No free lunch – a new inclusion list design
by vitalik & mike
august 15, 2023
\cdot
tl;dr; The free data availability problem is the core limitation of many inclusion list instantiations. We outline the mechanics of a new design under which the inclusion list is split into a Summary, which the proposer signs over, and a list of Txns, which remain unsigned. By walking through the lifecycle of this new inclusion list, we show that the free data availability problem is solved, while the commitments of the inclusion list are enforceable by the state-transition function. We conclude by modifying the design to be more data efficient.
\cdot
Contents
- The free data availability problem
- Core mechanics
- Solving the data efficiency problem
- FAQ
- Appendix 1:
Rebuilderencoding strategy - Appendix 2:
ReducedSummarystuffing
\cdot
Related work
- State of research: increasing censorship resistance of transactions under proposer/builder separation (PBS) by Vitalik – Jan 2022.
- How much can we constrain builders without bringing back heavy burdens to proposers? by Vitalik – Oct 2022.
- PBS censorship-resistance alternatives by Francesco – Oct 2022.
- Forward inclusion list by Francesco – Nov 2022.
- Censorship Résistance & PBS by Justin – Sept 2022.
- Censorship Resistance: crlists in mev-boost by Quintus – July 2022.
\cdot
Acronyms & abbreviations
| source | expansion |
|---|---|
IL |
inclusion list |
DA |
data availability |
Txns |
transactions |
\cdot
Thanks
Many thanks to Justin and Barnabé for comments on the draft. Additional thanks to Jon, Hasu, Tomasz, Chris, Toni, Terence, Potuz, Dankrad, and Danny for relevant discussions.
1. The free data availability problem
As outlined in Vitalik’s State of research piece, one of the key desiderata of an anti-censorship scheme is not providing free data availability (abbr. DA). Francesco’s Forward Inclusion List proposal addresses this by not incorporating data about the inclusion list (abbr. IL) into any block. The slot n IL is enforced by the slot n+1 attesting committee based on their local view of the p2p data. While this is an elegant solution that eliminates the free DA problem, it is a subjective enforcement of the IL. A non-conformant block can still become canonical if, for example, the slot n+1 attesters collude to censor by pretending to not see the IL on time. Additionally, it adds another sub-slot synchrony point to the protocol, as a deadline for the availability of the IL must be set.
Ideally, we want objective enforcement of the IL. It should be impossible to produce a valid block that doesn’t conform to the constraints set out in the IL. The naïve solution is to place the IL into the block body for slot n, allowing slot n+1 attesters can use the data as part of their state-transition function. This is objective because any block that doesn’t conform to the IL would be seen as invalid, and thus could not become canonical. Unfortunately, this idea falls victim to the free DA problem.
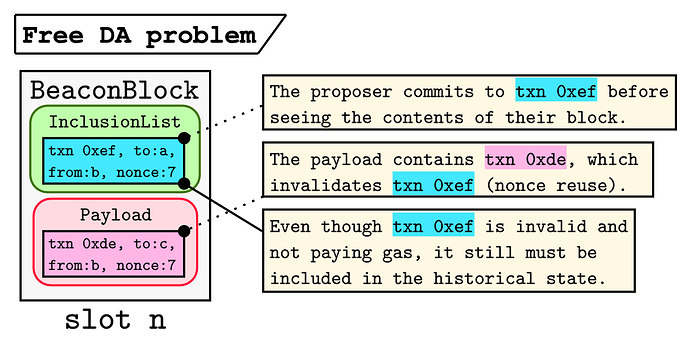
The key issue here is that a proposer must be able to commit to their IL before seeing the contents of their block. The reason is simple: in proposer-builder separations (PBS) schemes (mev-boost today, potentially ePBS in the future) the proposer has to commit to their block before receiving its contents to protect the builder from MEV stealing. Because the proposer blindly commits to their block, we cannot enforce that all of the transactions in the IL are valid after the slot n payload is executed. The figure below depicts an example:
Here the proposer commits to an IL which includes txn 0xef, which is from: b with nonce: 7. Unfortunately (or perhaps intentionally), the payload for their slot includes txn 0xde which is also from: b with nonce: 7. Thus txn 0xef is no longer valid and won’t pay gas, even if it is much larger than txn 0xde; getting txn 0xef into the IL but not the block itself may offer extreme gas savings by not requiring that the originator pays for the calldata stored with the transaction. However, since it is part of the state-transition function, it must be available in the chain history.
(Observation 1) Any inclusion list scheme that
- allows proposers to commit to specific transactions before seeing their payload, and
- relies on the state-transition function to enforce the IL commitments,
admits free DA.
The reasoning here is quite simple – if the conditions of (Obs. 1) are met, the contents of the IL transactions must be available to validate the block. Even if the block only committed to a hash of the IL transaction, we still need to see the full transaction in the clear for the state-transition function to be deterministic.
2. Core mechanics
To solve the free DA problem, we begin by specifying the building blocks of the new IL design and lifecycle, which is split into the construction, inclusion, and validation phases.
Definitions
slot npre-state – The execution-layer state before theslot npayload is executed (i.e., the state based on the parent block).slot npost-state – The execution-layer state after theslot npayload is executed.InclusionList (abbr. IL)– The transactions and associated metadata that aslot nproposer constructs to enforce validity conditions on theslot n+1block. The IL is decomposed into two, equal-length lists –SummaryandTxns.Summary– A list of(address, gasLimit)pairs, which specify thefromandgasLimitof each transaction inTxns. Each pair is referred to as anEntry.Txns– A list of full transactions corresponding to the metadata specified in theSummary. These transactions must be valid in theslot npre-state and have amaxFeePerGasgreater than theslot nblock base fee times 1.125 (to account for the possible base fee increase in the next block).Entry– A specific(address, gasLimit)element in theSummary. AnEntryrepresents a commitment to a transaction fromaddressgetting included either inslot norn+1as long as the remaining gas in theslot n+1payload is less thangasLimit.Entrysatisfaction – AnEntrycan be satisfied in one of three ways:
1. a transaction fromaddressis included in theslot npayload,
2. a transaction fromaddressis included in theslot n+1payload, or
3. the gas remaining (i.e., theblock.gasLimitminus gas used) in theslot n+1payload is less than thegasLimit.
(Observation 2) A transaction that is valid in the
slot npre-state will be invalid in theslot npost-state if
- the
slot npayload includes at least one transaction from the same address (nonce reuse) or- the
maxFeePerGasis less than the base fee of the subsequent block.
While transactions may fail for exogenous reasons (e.g., the price on a uniswap pool moving outside of the slippage set by the original transaction), they remain valid.
Inclusion list lifecycle
We now present the new IL design (this is a slightly simplified version – we add a few additional features later). Using slot n as the starting point, we split the IL lifecycle into three phases. The slot n proposer performs the construction, the slot n+1 proposer does the inclusion, and the entire network does the validation. Each phase is detailed below.
- Construction – The proposer for
slot nconstructs at least oneIL = Summary + Txns, and signs theSummary(the fact that the proposer can construct multiple ILs is important).- The transactions in
Txnsmust be valid based on theslot npre-state (and have a high enoughmaxFeePerGas), but the proposer does not sign over them. - The proposer then gossips an object containing:
- their
SignedBeaconBlock, and - their
IL = Summary (signed) + Txns (unsigned).
- their
- Both the block and an IL must be present in the validator’s view to consider the block as eligible for the fork-choice rule.
- The transactions in
- Inclusion – The proposer for
slot n+1creates a block that conforms to aSummarythat they have observed (there must be at least one for them to build on that block).- The
slot n+1block includes aslot nSummaryalong with the signature from theslot nproposer.
- The
- Validation – The network validates the block using the state-transition function.
- Each
Entryin theSummarymust be satisfied for the block to be valid. - The signature over the
Summarymust be valid.
- Each
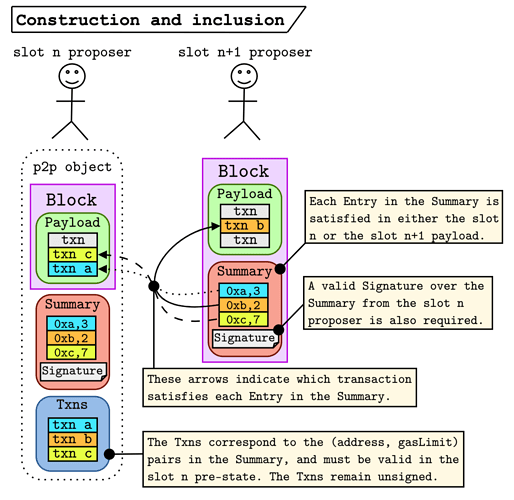
Wait… that’s it? yup ![]() (well this solves the free DA problem – we introduce a few extra tricks later, but this is the gist of it). The figure below shows the construction and inclusion stages.
(well this solves the free DA problem – we introduce a few extra tricks later, but this is the gist of it). The figure below shows the construction and inclusion stages.
- The
slot nproposer signs theSummary=[(0xa, 3), (0xb, 2), (0xc, 7)]and broadcasts it along withTxns = [txn a, txn b, txn c]. - The
slot npayload includestxn candtxn a(order doesn’t matter). These transactions satisfy(0xc, 7)and(0xa, 3)respectively. - The
slot n+1proposer sees that the only entry that they need to satisfy in their payload is(0xb, 2), which they do by includingtxn b. - The rest of the network checks that each
Entryis satisfied and that the signature over theSummaryis valid.
Validators require that there exists at least one valid IL before they consider the block for the fork-choice rule. If a malicious proposer publishes a block without a corresponding IL=Summary+Txns, the honest attesters in their slot (and future slots) will vote against the block because they don’t have an available IL.
How does that solve the free DA problem?
Two important facts allow this scheme to avoid admitting free DA.
- Potential for multiple ILs. Since the proposer doesn’t include anything about their IL in their block, they can create multiple without committing a proposer equivocation.
- Reduced specificity of the
ILcommitments. TheSummarycan be satisfied by a transaction in either theslot nor theslot n+1payload and the transaction that satisfies a specificEntryin theSummaryneedn’t be the same transaction that accompanied theSummaryin theTxnslist.
By signing over the list of (address, gasLimit) pairs, the proposer is saying: “I commit that during slot n or slot n+1, a transaction from address will be included as long as the remaining gas in the slot n+1 payload is less than gasLimit.”
By not committing to a specific set of transactions, the slot n proposer gives the network deniability. This concept relates to cryptographic deniability in that validators can deny having received a transaction without an adversary being able to disprove that. This property follows from the observation below.
(Observation 3) The only way to achieve free DA is by sending multiple transactions from the same address with the same nonce.
Recall that the free DA problem arises when a transaction that was valid in the slot n pre-state is no longer valid in the slot n post-state but is still committed to in the inclusion list. From (Obs. 2), the only way this can happen is through nonce reuse (the base fee is covered by requiring the transactions to have 12.5% higher maxFeePerGas than the current block base fee). This leads to the final observation.
(Observation 4) If
txn baims to achieve free DA, then there exists atxn asuch thattxn asatisfies the sameEntryin theSummaryastxn b. Thus validators can safely deny having seentxn b, because they can claim to have seentxn ainstead.
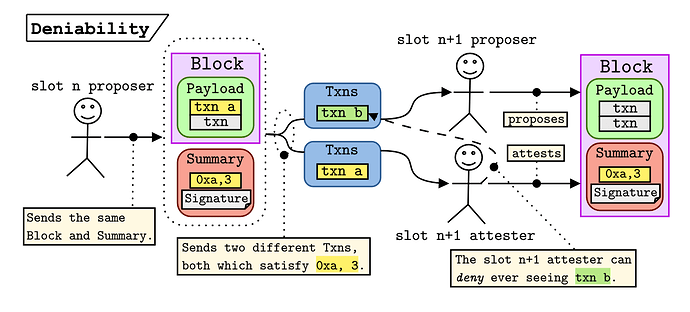
In other words, validators don’t have to store the contents of any transactions that don’t make it on chain, and the state-transition function is still deterministic. The figure below encapsulates this deniability.
- The
slot nproposer creates theirBlockandSummary. They notice thattxn aandtxn bare both valid at theslot npre-state and satisfy theEntry0xa, 3. - The
slot nproposer distributes two versions ofTxns, one with each transaction. - The
slot n+1proposer sees thattxn bis invalid in theslot npost state (becausetxn a, which is also from the0xaaddress, is in theslot npayload). - The
slot n+1proposer constructs their block with theSummary, but safely dropstxn b, becausetxn asatisfies theEntry. - The
slot n+1attester includes the block in their view because they have seen a valid IL (where theTxnsobject containstxn a). - The
slot n+1attester verifies the signature and confirms that theEntryis satisfied. - Key point – the
slot n+1attester never sawtxn b, but they are still able to verify theslot n+1block. This implies that the attester can credibly deny havingtxn bavailable.
Thus txn b can safely be dropped from the beacon nodes because it is not needed for the state-transition function; txn b is no longer available. This example is slightly simplified in that txn a and txn b are both satisfied by the same Entry in the Summary (meaning they have the same gasLimit). With different gasLimit values, the slot n proposer would need to create and sign multiple Summary objects, which is fine because the Summary is not part of their block.
3. Solving the data efficiency problem
The design above solves the free DA problem, but it introduces a new (smaller) problem around data efficiency. The slot n+1 proposer includes the entire slot n Summary in their block. With 30M gas available and the minimum transaction consuming 21k gas, a block could have up to 1428 transactions. Thus the Summary could have 1428 entries, each of which consumes 20 (address) + 1 (gasLimit) bytes (using a single byte to represent the gasLimit in the Summary). This implies that the Summary could be up to 29988 bytes, which is a lot of additional data for each block. Based on the fact that each Entry in the Summary is either satisfied in slot n or slot n+1, we decompose the Summary object into two components:
ReducedSummary– the remainingEntryvalues that are not satisfied by theslot npayload, andRebuilder– an array used to indicate which transactions in theslot npayload satisfyEntryvalues in the originalSummary.
The slot n+1 proposer only needs to include the ReducedSummary and the Rebuilder for the rest of the network to reconstruct the full Summary. With the full Summary, the slot n proposer signature can be verified as part of the slot n+1 block validation.
What the heck is the “Rebuilder”?
The Rebuilder is a (likely sparse) array with the same length as the number of transactions in the slot n payload. For each index i:
Rebuilder[i] = 0implies that theithtransaction of theslot npayload can be ignored.Rebuilder[i] = x, wherex !=0implies that theithtransaction of theslot npayload corresponds to anEntryin the signedSummary, wherexindicates thegasLimitfrom the originalEntry.
Now the algorithm to reconstruct the original Summary is as follows:
ReconstructedEntries = []
for i in range(len(Rebuilder)):
if Rebuilder[i] != 0:
ReconstructedEntries.append(
Entry(
address=SlotNPayload[i].address,
gasLimit=Rebuilder[i]
)
)
Summary = sorted(ReducedSummary.Extend(ReconstructedEntries))
The Summary needs some deterministic order to verify the slot n proposer signature. The easiest solution is to simply sort based on the address of each Entry. We can further reduce the amount of data in the Rebuilder by representing the gasLimit with a uint8 rather than a full uint32.
Inclusion list lifecycle (revisited)
The IL lifecycle largely remains the same, but it is probably worth revisiting it with the addition of the ReducedSummary and Rebuilder.
- (unchanged) Construction – The proposer for
slot nconstructs at least oneIL = Summary + Txns, and signs theSummary(the fact that the proposer can sign multiple ILs is important).- The transactions in
Txnsmust be valid based on theslot npre-state (and have a high enoughmaxFeePerGas), but the proposer does not sign over them. - The proposer then gossips an object containing:
- their
SignedBeaconBlock, and - their
IL = Summary (signed) + Txns (unsigned).
- their
- Both the block and an IL must be present in the validator’s view to consider the block as eligible for the fork-choice rule.
- The transactions in
- (changed) Inclusion – The proposer for
slot n+1creates a block that conforms to theSummarythey have observed.- They construct the
ReducedSummaryandRebuilderbased on theslot npayload. - The block includes the
ReducedSummary,Rebuilder, and the original signature from theslot nproposer.
- They construct the
- (changed) Validation – The network validates the block using the state-transition function.
- The full
Summaryis reconstructed using theReducedSummaryand theRebuilder. - The
slot nproposer signature is verified against the fullSummary. - Each
Entryin theSummarymust be satisfied for the block to be valid.
- The full
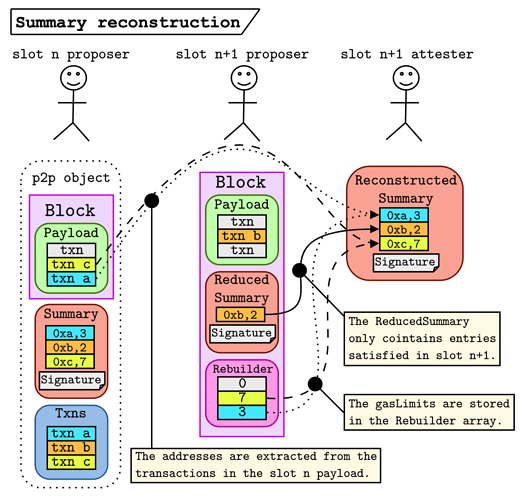
The figure below demonstrates this process.
- (unchanged) The
slot nproposer signs theSummary=[(0xa, 3), (0xb, 2), (0xc, 7)]and broadcasts it along withTxns = [txn a, txn b, txn c], which must be valid in theslot npre-state. - (unchanged) The
slot npayload includestxn candtxn a(order doesn’t matter). - (changed) The
slot n+1proposer sees that entries0,2in theSummaryare satisfied, so makes theReducedSummary=(0xb, 2). This is the only entry that they need to satisfy inslot n+1, which they do by includingtxn bin their payload. - (changed) The
slot n+1proposer constructs theRebuilderby referencing the transaction indices in theslot npayload needed to recover the addresses. TheRebuilderarray also contains the originalgasLimitvalues that theslot n+1proposer received. - (changed) The
slot n+1attesters use theRebuilder, theReducedSummary, and theslot npayload to reconstruct the fullSummaryobject to verify the signature.
This scheme takes advantage of the fact that most of the Summary data (the address of each Entry satisfied in slot n) will be already stored in the slot n payload. Rather than storing these addresses twice, the Rebuilder acts as a pointer to the existing data. The Rebuilder needs to store the gasLimit of each original Entry because the transaction in the slot n payload may be different than what originally came in the Txns.
*-thanks for reading! ![]()
![]() -*
-*
FAQ
- What is the deal with the
maxFeePerGas?- One of the transaction fields is
maxFeePerGas. This specifies how much the transaction is willing to pay for the base fee. To ensure the transaction is valid in theslot npost-state, we need to enforce that themaxFeePerGasis at least 12.5% (the max amount the base fee can increase from block to block) higher than the current base fee.
- One of the transaction fields is
- Why do we need to include the
ReducedSummaryin theslot n+1payload?- We technically don’t! We could use a
Rebuilderstructure to recover theSummaryentries that are satisfied in theslot n+1payload as well. It is just a little extra complexity that we didn’t think was necessary for this post. This ultimately comes down to an implementation decision that we can make.
- We technically don’t! We could use a
- What happens if a proposer never publishes their IL, but gets still accumulates malicious fork-choice votes on their block?
- Part of the honest behavior of accepting a block into their fork-choice view is that a valid IL accompanies it. Even if the malicious attesters vote for a block that doesn’t have an IL, all of the subsequent honest attesters will vote against that fork based on not seeing the IL.
- Can the
slot nproposer play timing games with the release of their IL?- Yes, but no more than they can do already. It is the same as if the
slot nproposer tried to grief theslot n+1proposer by not sending them the block in time. They risk not accumulating enough attestations to overpower the proposer boost of the subsequent slot.
- Yes, but no more than they can do already. It is the same as if the
- What happens if a proposer credibly commits (e.g., through the use of a TEE) to only signing a single
Summary?- Justin came up with a scenario where a proposer and a transaction originator can collude to get a single valid
Summarypublished (e.g., by using a TEE) that has anEntrythat is only satisfied by a single transaction. This would break the free DA in that all honest attesters would need to see this transaction as part of the IL they require to accept the block into their fork-choice view. We can avoid this by allowing anyone to sign arbitrarySummaryobjects for any slot that is at least n slots in the past. The default behavior could be for some validators to simply sign emptySummaryobjects after 5 slots have passed.
- Justin came up with a scenario where a proposer and a transaction originator can collude to get a single valid
- How does a sync work with the IL?
- This is related to the question above, because seeing a block as valid in the fork-choice view requires a full IL for that slot. If we allow anyone to sign ILs for past slots, the syncing node can simply sign ILs for each historical slot until it reaches the head of the chain.
- Why use
uint8instead ofuint32for the gas limits in theSummary?- This is just a small optimization to reduce the potential size of the maximum
Summaryby a factor of four. The constraint would be that theTxnsmust use less than or equal to the uint8gasLimitspecified in the corresponding entry. This becomes an implementation decision as well.
- This is just a small optimization to reduce the potential size of the maximum
Appendix 1: Rebuilder encoding strategy
The slot n proposer has control over some of the data that ends up in the slot n+1 Rebuilder, and thus can use it to achieve a small amount of free DA (up to 1428 bits = 178.5 bytes). The technique is quite simple. Let’s use the case where the proposer’s payload contains 1000 transactions, which allows the proposer to store a 1000-bit message for free, denoted msg. Let payload[i] and msg[i] denote the ith transaction in their payload and the ith bit in the message respectively.
- The
slot nproposer self-builds a block, thus they know the contents of the block before creating theirSummary. - To construct their
Summary, for each indexi, do- if
msg[i] == 0, don’t includepayload[i]in theSummary. - if
msg[i] == 1, includepayload[i]in theSummary.
- if
It follows that by casting Rebuilder from a byte array to a bit array, msg is recovered. Since the Rebuilder is part of the slot n+1 block, msg is encoded into the historical state. However, the fact that this is at most 178.5 bytes per block makes it unlikely to be an attractive source of DA. Additionally, it’s only possible to store as many bits as there are valid transactions to include in the slot n payload. The maximum is 1428 if each transaction is a simple transfer, but historically blocks contain closer to 150-200 transactions on average.
Appendix 2: ReducedSummary stuffing
It is also worth considering the case where the slot n proposer tries to ensure that the slot n+1 ReducedSummary is large. The most they can do is self-build an empty block while putting every valid transaction they see into their Summary object. With an empty block, the slot n+1 ReducedSummary is equivalent to the slot n Summary (because none of the entries have been satisfied in the slot n payload). As we calculated above, the max size of the ReducedSummary would be 29988 bytes, which is rather large, but only achievable if there are 1428 transfers lying around in the mempool. Even if that happens, the slot n proposer just gave up all of their execution layer rewards to make the next block (at most) 30kB larger. Blocks can already be much larger than that (some are hundreds of kB), and post-4844, this will be even less relevant. Thus this doesn’t seem like a real griefing vector to be concerned about. We also could simply use a Rebuilder for the slot n+1 payload as well if necessary.