The protocol under/over reacts to changes in block times. Worth Fixing?

Economics
1

A few weeks ago I plotted Blocktimes overtime and noticed a pattern. The past few days I have been working on calculations around the difficulty bomb at the Status Hackathon. While working I observed a few more related pieces and after talking to a few people here, was recommended to post for additional feedback. I am not sure the significance of these findings from a Tokenomic incentives perspective, and would appreciate feedback and validation/invalidation of the underlying ideas.

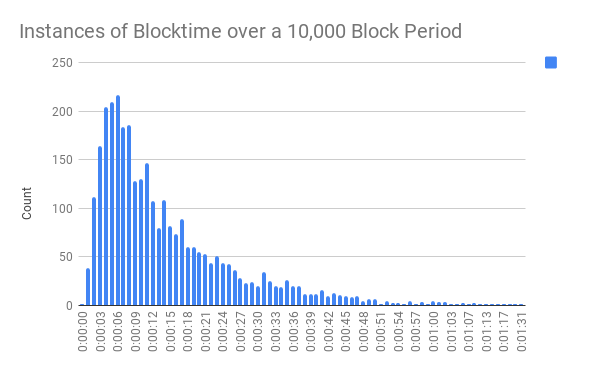
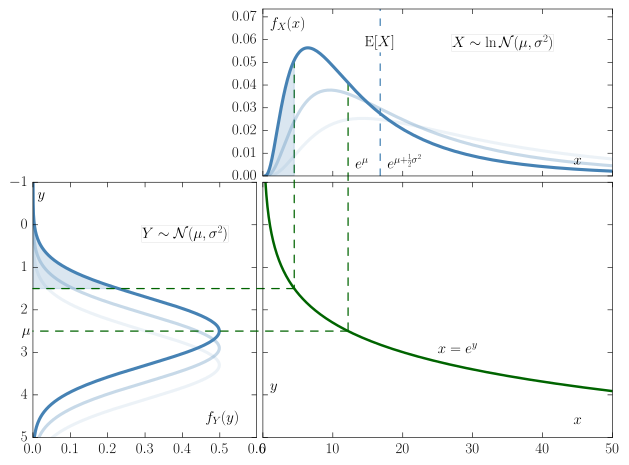
The probability distribution of block times is a [Log-Normal Distribution](https://en.wikipedia.org/wiki/Log-normal_distribution)

Most often when dealing with probabilities we see a Normal Distribution. At first thought it is easy to think that BlockTime fits into this as well, but it in fact does not. Logically, it can be seen because you are unable to have a Blocktime of less then zero on one end and on the other a blocktime can be of any length (all though very unlikely to be extremely long). You can also see this in the data. The chart below is distribution of blocktimes over 10,000 blocks starting on Sep-08-2018 12:53:38 PM +UTC
image

** The Difficulty Function Adapts Linearly **

The correction factor in the difficulty adapting equation responds linearly in respect to block time. Why may this be a problem?

** The probability that a blocktime occurs is an exponential function, but the function that responds to changes in blocktime reacts linearly **

If the claims are true the function adapting the difficulty target would under react or over react to changes in block time.

Some possible consequences:

  • Oscillations in difficulty and blocktime. Eventually the linear function catches up and explains the stability of blocktimes over large enough periods of time.
  • The existence of a “sweet spot” where there is an ideal acceleration or deceleration of Hashrate in order to maximize accumulation of coins over time.

My conclusion is that if we had a difficulty function that adapts to how statistically unlikely a block time is to occur that the blockchain would be more robust and stable against increases and decreases in Hashrate.

Feedback and correction is welcome and preferred. I am not a trained mathematician, just a musician that loves numbers and hopes any of these observations can help.

Cheers,
James

1 Like
2

As a new user I was unable to add in a few other images I would have liked to include.

Here is one where you can see the relation between a log-normal and a normal distribution. It also shows the underlying exponential function.

image

3

As well as equations for difficulty calculation from the yellow paper.

image
image1026Ă—577 70.7 KB

4

image
image675Ă—577 54.9 KB

5

Technically, block times should be a Poisson distribution. The reason why they are not is network latency. Hence, instead what I think we’re seeing is the distribution of x+y, where x (latency) is a normal distribution and y (time to mine after seeing the parent block) is a Poisson distribution.

This seems to suggest network latency is somewhere around 3 seconds, which seems to confirm where the ~15-20% uncle rate is coming from.

6

Oh, I hadn’t considered the latency of discovery affecting the distribution. This makes a lot more sense as it was difficult to fit it to one such model because it was the combination of two!

Has anyone deployed a local Ethereum instance and mined it with a fixed hash rate? I am curious what the function that models Ethereum’s blocks actually would be without the latency affecting it.

And a followup question, a Poisson Distribution is also not a linear function. So perhaps is still worth looking at the difficulty adjustment equations to match it more closely?

7

Ah sorry, I meant Poisson process, with an exponential distribution. This one: https://en.wikipedia.org/wiki/Exponential_distribution

1 Like
8

This is only for POW, correct? This would change with POS?

9

Yes. Once block producers are known in advance block production is no longer random and will vary only by network latency.

1 Like