Using GKR inside a SNARK to reduce the cost of hash verification down to 3 constraints (1/2)
Alexandre Belling, Olivier Bégassat
Link to HackMD document with proper math equation rendering
Large arithmetic circuits C (e.g. for rollup root hash updates) have their costs mostly driven by the following primitives:
- Hashing (e.g. Merkle proofs, Fiat-Shamir needs)
- Binary operations (e.g. RSA, rangeproofs)
- Elliptic curve group operations (e.g. signature verification)
- Pairings (e.g. BLS, recursive SNARKs)
- RSA group operations (e.g. RSA accumulators)
Recent efforts achieved important speed-ups for some of those primitives. Bünz et al. discovered an inner-product pairing argument which provide a way to check a very large number of pairing equation in logarithmic time. It can be used as an intermediate argument to run BLS signature and pairing-based arguments (PLONK, Groth16, Marlin) verifiers for very cheap although it requires a curve enabling recursion and an updatable trusted setup. Ozdemir et al, and Plookup made breakthrough progresses to make RSA operation practical inside an arithmetic circuit, and more generally arbitrary-size big-integer arithmetic.
In order to make cryptographic accumulators practical, recents works suggests the use of RSA accumulators.
We propose an approach to speed-up proving for hashes based on the line of work of GKR/Giraffe/Hyrax/Libra. It yields an asymptotic speed-up of \times700/3 (more than \times200) for proving hashes: 3 constraints for hashing 2 elements with gMIMC compared to ~700 without.
We start by describing the classic sumcheck and GKR protocols. Readers familiar with these may skip the “background section” altogether. We then introduce some modifications to tailor it for hash functions. Our current main use-case is making merkle-proof verifications cheap in rollups. Similar constructions could be achieved for other use-cases.
Background
This section gives a high-level description of the GKR protocol: a multi-round interactive protocol whereby a prover can convince a verifier of a computation y=C(x). GKR builds on top of the sumcheck protocol so we describe that protocol as well.
GKR makes no cryptographic assumptions. Moreover, it has the interesting feature that it’s prover-time is several orders of magnitude more efficient than pairing-based SNARK. More precisely, we describe Gir++ (cf. Hyrax paper), a variant on GKR specialized for data-parallel computation, e.g. for circuits computing multiple parallel executions of a given subcircuit.
Arithmetic circuits
Consider first a small base circuit C_0 : a layered arithmetic circuit where
- each gate is either an addition gate or a multiplication gate,
- each gate has 2 inputs (i.e. fan-in 2 and unrestricted fan-out)
- the outputs of layer i become the inputs of layer i-1.
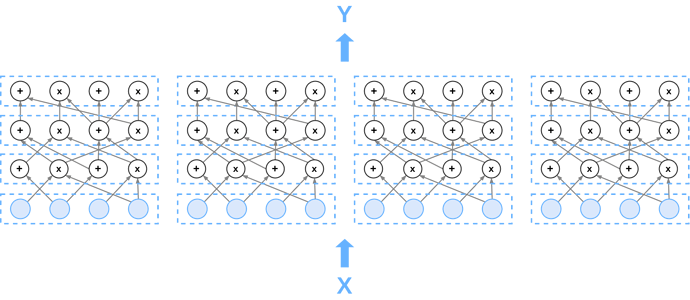
The geometry of such a circuit is described by its width G, its depth d and the wiring (which layer i-1 outputs get funneled into which layer i gates). Thus the base circuit takes inputs x\in\Bbb{F}^G (at layer 0) and produces outputs y\in\Bbb{F}^G (at layer d): y=C_0(x). The base circuit C_0 represents a computation for which one wishes to provide batch proofs.
In what follows we will concern ourselves with arithmetic circuits C comprised of the side-by-side juxtaposition of N identical copies of the base circuit C_0. Thus C represents N parallel executions of the base circuit C_0.The circuit thus takes a vector x \in \mathbb{F}^{N \times G} as input and produces an output y \in \mathbb{F}^{N \times G}.
We’ll make some simplifying (but not strictly necessary) assumptions:
- the width of the base circuit is the same at every layer,
- in particular, inputs (x) and outputs (y) have the same size,
- both G = 2^{b_G} and N = 2^{b_N} are powers of 2.
Arithmetization
The Gir++ protocol provides and argument for the relation: R_L = \Big\{(x, y) \in (\mathbb{F}^{N \times G})^2~\Big|~ y = C(x)\Big\}
Describing the protocol requires one to define a certain number of functions. These functions capture either the geometry of the circuit or the values flowing through it. To make matters precise, we consistently use the following notations for input variables
- q'\in\{0, 1\}^{b_N} is the index of one of the N identical copies of the base circuit C_0 within C,
- q\in \{0, 1\}^{b_G} is a “horizontal index” within the base circuit,
- i\in [d]=\{0,1,\dots,d\} is a layer (“vertical index”) within the base circuit.
This makes most sense if one thinks of the subcircuit as a “matrix of arithmetic gates”. Thus a pair (q,i) describes the position of a particular arithmetic gate in the base circuit, and a triple (q',q,i) describes the arithmetic gate at position (q,i) in the q'-th copy of the base circuit C_0 within C.
- h'\in\{0, 1\}^{b_N} represents the index of a copy of the base circuit within C
- h_L,h_R\in\{0, 1\}^{b_G} represent two “horizontal indices” in the base circuit.
With that notation out of the way, we describe various functions. The first lot describes the circuit geometry. Recall that all gates are fan-in 2:
- add_i(q, h_L, h_R) = 1 iff the gate q at layer i takes both h_L and h_R as inputs from layer i - 1 and is an addition gate. Otherwise add_i(q, h_L, h_R) = 0.
- mul_i(q, h_L, h_R) = 1 if the gate q at layer i takes both h_L and h_R as inputs from layer i - 1 and is an multiplication gate. Otherwise mult_i(q, h_L, h_R) = 0.
- eq(a, b) returns a == b
Next we introduce functions that captures the values that flow through the circuit:
- V_i(q', q) is the output value of the gate at position (q,i) in the q'-th copy of the base circuit C_0 within C.
The \Bbb{F}-valued function below captures transition from one layer to the next:
- P_{q', q, i}(h', h_L, h_R) = eq(h',q') \cdot \left[ \begin{array}{r} add_i(q, h_L, h_R)\cdot(V_{i-1}(q', h_L) + V_{i-1}(q', h_R))\\+\;mul_i(q, h_L, h_R)\cdot V_{i-1}(q', h_L)\cdot V_{i-1}(q', h_R)\end{array}\right].
It holds that V_i(q',q) = \sum_{h' \in \{0, 1\}^{b_N}}\sum_{h_L< h_R \in \{0, 1\}^{b_G}}P_{q', q, i}(h', h_L, h_R) This is not complicated to see: the RHS of this equation contains at most one nonzero term.
Key observation. V_i is expressed as an exponentially large sum of values of the function of V_{i-1}. The sumcheck protocol described in the next section provides polynomial time verifiable proofs for assertions of the form
\displaystyle\qquad\qquad\texttt{(some claimed value)} =\sum_{x\in\left\{\begin{array}{c}\text{exponentially}\\ \text{large domain}\end{array}\right\}}f(x)
for domains of a “specific shape” and “low degree” functions f:\Bbb{F}^n\to\Bbb{F}. This gives rise to a proof system for R_L.
The sumcheck protocol: setting up some notation
This section describes the sumcheck protocol. It is a central piece of how Gir++ works.
Multilinear polynomials are multivariate polynomials P(X_1,\dots,X_n)\in\Bbb{F}[X_1,\dots,X_n] that are of degree at most 1 in each variable. e.g.: P(U,V,W,X,Y,Z)=3 + XY + Z -12 UVXZ +7 YUZ (it has degree 1 relative to U,V,X,Y,Z and degree 0 relative to W). In general, a multilinear polynomial is a multivariate polynomial of the form P(X_1, X_2\dots, X_{d}) = \sum_{i_1 \in \{0, 1\}}\sum_{i_2 \in \{0, 1\}}\cdots\sum_{i_{d} \in \{0, 1\}} a_{i_1, i_2, \dots, i_{d}} \prod_{k=1}^{d} X_k^{i_k} with field coefficients a_{i_1, i_2, \dots, i_{d}}\in\Bbb{F}.
Interpolation. Let f: \{0,1\}^d \rightarrow \mathbb{F} be any function. There is a unique multilinear polynomial P_f=P_f(X_1,\dots,X_d) that interpolates f on \{0_\mathbb{F}, 1_\mathbb{F}\}^d. Call it the arithmetization of f. For instance P(X,Y,Z)=X+Y+Z-YZ-ZX-XY+XYZ is the arithmetization of f(x,y,z)=x\vee y\vee z (the inclusive OR).
In the following we will sometimes use the same notation for a boolean function f and its arithmetization P_f. This is very convenient as it allows us to evaluate a boolean function \{0,1\}^d\to\Bbb{F} on the much larger domain \Bbb{F}^d. This is key to the sumcheck protocol described below.
Partial sum polynomials. If P\in\Bbb{F}[X_1,\dots,X_d] is a multivariate polynomial, we set, for any i=1,\dots,d, P_i \in\Bbb{F}[X_1,\dots,X_i] defined by P_i(X_1, ..., X_i) = \sum_{b_{i+1}, \dots, b_d\in\{0,1\}} P(X_1,\dots,X_i,b_{i+1},\dots,b_d) the partial sums of P on the hypercube \{0, 1\}^{d-i}. We have P_d = P. Note that each P_i is of degree \leq \mu in each variable.
The sumcheck protocol: what it does
The (barebones) sumcheck protocol allows a prover to produce polynomial time checkable probabilistic proofs of the language R_L = \Big\{(f,a) ~\Big|~ f:\{0,1\}^d \rightarrow \mathbb{F} \text{ and }a \in \mathbb{F} \text{ satisfy } \sum_{x \in \{0, 1\}^d} f(x) = a\Big\} given that the verifier can compute the multilinear extension of f (directly or by oracle access). Verifier time is O(d + t) where t is the evaluation cost of P. The protocol transfers the cost of evaluating the P=P_f on the whole (exponential size) boolean domain to evaluating it at a single random point \in\Bbb{F}^d.
Note: the sumcheck protocol works more broadly for any previously agreed upon, uniformly “low-degree in all variables” multivariate polynomial P which interpolates f on its domain. The only important requirement is that P be low degree in each variable, say \deg_{X_i}(P)\leq \mu for all i=1,\dots,d and for a “small” constant \mu. In the case of multilinear interpolation of f one has \mu=1, but it can be useful (and more natural) to allow larger \mu depending on the context (e.g. GKR).
We actually need a variant of this protocol for the relation R_L = \left\{(f_1, f_2, f_3,a) ~\left|~ \begin{array}{l}f_1,f_2,f_3:\{0,1\}^d \rightarrow \mathbb{F} \text{, } a \in \Bbb{F}\\\text{ satisfy } \displaystyle\sum_{x \in \{0, 1\}^d} f_1(x)f_2(x)f_3(x) = a\end{array}\right.\right\}. This changes things slightly as we will need to work with multivariate polynomials of degree \leq 3 in each variable. To keep things uniform, we suppose we are summing the values of a single function f (or a low-degree interpolation P thereof) over the hypercube \{0,1\}^d which is of degree \leq \mu in all d variables. e.g. for us f=f_1f_2f_3, P=P_{f_1}P_{f_2}P_{f_3} and \mu=3. The sumcheck protocol provides polynomial time checkable probabilistic proofs with runtime O(\mu d + t).
The sumcheck protocol: the protocol
The sumcheck protocol is a multi-round, interactive protocol. It consists of d rounds doing ostensibly the same thing (from the verifier’s point of view) and a special final round.
At the beginning, the verifier sets a_0 := a, where a is the claimed value of the sum of the values of f (i.e. of a uniformly low-degree extension P of f) over the hypercube \{0,1\}^d.
Round 1
- The prover sends P_1(X_1) (univariate, of degree at most \mu), i.e. a list of \mu+1 coefficients in \Bbb{F}.
- The verifier checks that P_1(0) + P_1(1) = a_0.
- The verifier randomly samples \eta_1\in\Bbb{F}, sends it to the prover and computes a_1 = P_1(\eta_1).
The next rounds follow the same structure.
Round i\geq 2
- The prover sends P_i(\eta_1,\dots,\eta_{i-1},X_i) (univariate, of degree at most \mu), i.e. a list of \mu+1 coefficients in \Bbb{F}.
- The verifier checks that P_i(0) + P_i(1) = a_{i-1}.
- The verifier randomly samples \eta_i\in\Bbb{F}, sends it to the prover and computes a_i = P_i(\eta_i).
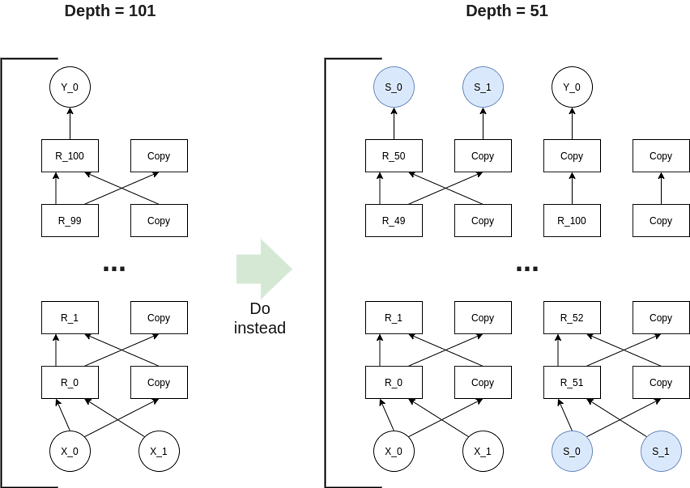
Giraffe describes a refinement to compute the evaluations of p_i in such a way the prover time remains linear in the number of gates: link to the paper. Libra also proposes an approach in the general case (meaning even if we don’t have data-parallel computation)
Special final round
The verifier checks (either direct computation or through oracle access) that P_{d}(\eta_{d})\overset?=P(\eta_1, \dots, \eta_{d}). In some applications it is feasible for the verifier to evaluate P directly. In most cases this is too expensive.
The sumcheck protocol reduces a claim about an exponential size sum of values of P to a claim on a single evaluation of P at a random point.
The GKR protocol
The GKR protocol produces polynomial time verifiable proofs for the execution of a layered arithmetic circuit C. It does this by implementing a sequence of sumcheck protocols. Each iteration of the sumcheck protocol inside GKR establishes “consistency” between two successive layers of the computation (starting with the output layer, layer 0, and working backwards to the input layer, layer d). Every run of the sumcheck protocol a priori requires the verifier to perform a costly polynomial interpolation (the special final round). GKR bysteps this completely: the prover-provides the (supposed) value of that interpolation, and another instance of the sumcheck protocol is invoked to prove the correctness of this value. In GKR, the only time the final round of the sumcheck protocol is performed by the verifier is at the final layer (layer d: input layer).
The key to applying the sumcheck protocol in the context of the arithmetization described earlier for a layered, parallel circuit C is the relation linking the maps V_i, P_{q', q, i} and V_{i-1} (here these maps are identified with the appropriate low-degree extensions). Establishing consistency between two successive layers of the GKR circuit C takes up a complete sumcheck protocol run. Thus GKR proofs for a depth d circuit are made up of d successive sumcheck protocol runs.
The main computational cost for the prover is computing intermediate polynomials P_i. This cost can be made linear if P can be written as a product of multilinear polynomials as decribed in Libra by means of a bookkeeping table.
First round
- The verifier evaluates v_{d} = V_{d}(r_{d}', r_{d}) where (r_{d}', r_{d}) \in \mathbb{F}^{b_N + b_G} are random challenges. Then he sends r' and r to the prover. The evaluation of V_{d} can be done by interpolating the claimed output y.
- The prover and the verifier engages in a sumcheck protocol to prove that v_{d} is consistent with the values of the layer d-1. To do so, they use the relation we saw previously. V_i(q',q) = \sum_{h' \in \{0, 1\}^{b_N}}\sum_{h_L,h_R \in \{0, 1\}^{b_G}}P_{q', q, i}(h', h_L, h_R)
Important note. This is an equality of functions \{0,1\}^{b_N}\times\{0,1\}^{b_G}\to\Bbb{F}:
- on the LHS the map V_i(\bullet',\bullet)
- on the RHS the map \sum_{h' \in \{0, 1\}^{b_N}}\sum_{h_L,h_R \in \{0, 1\}^{b_G}}P_{\bullet', \bullet, i}(h', h_L, h_R)
Since we are going to try and apply the sumcheck protocol to this equality, we first need to extract from this equality of functions an equality between a field element on the LHS and an exponentially large sum of field elements on the RHS. This is done in two steps:
- multilinear interpolation of both the LHS and RHS to maps \Bbb{F}^{b_N}\times\Bbb{F}^{b_G}\to\Bbb{F},
- evaluation at some random point (Q',Q)\in\Bbb{F}^{b_N}\times\Bbb{F}^{b_G}
- sumcheck protocol invocation to establish V_i(Q',Q) = \sum_{h' \in \{0, 1\}^{b_N}}\sum_{h_L,h_R \in \{0, 1\}^{b_G}}P_{Q', Q, i}(h', h_L, h_R), which requires low degree interpolation of the map P_{Q', Q, i}(\bullet', \bullet_L, \bullet_R):\{0,1\}^{b_{N}}\times\{0,1\}^{b_{G}}\times \{0,1\}^{b_{G}}\to\Bbb{F}. This particular low degree-interpolation is systematically constructed as a product of multilinear interpolations of functions that together make up the map P_{\bullet', \bullet, i}(\bullet', \bullet_L, \bullet_R):\{0,1\}^{b_{N}}\times\{0,1\}^{b_{G}}\times\{0,1\}^{b_{N}}\times\{0,1\}^{b_{G}}\times \{0,1\}^{b_{G}}\to\Bbb{F}
We won’t bother further with the distinction (q,q')\in\{0,1\}^{b_N}\times\{0,1\}^{b_G} and (Q,Q')\in\Bbb{F}^{b_N}\times\Bbb{F}^{b_G}.
As a result, at the final round of the sumcheck, the verifier is left with a claim of the form P_{r_{d}', r_{d}, i}(r'_{d-1}, r_{L, d-1}, r_{R, d-1}) == a, where r'_{d-1}, r_{L, d-1} and r_{R, d-1} are the randomness generated from the sumcheck. Instead of directly running the evaluation (which requires knowledge of V_{d-2}), the verifier asks the prover to send evaluation claims of V_{d-1}(r'_{d-1}, r_{L, d-1}) and V_{d-1}(r'_{d-1}, r_{L, d-1}). The verifier can then check that those claims are consistent with the claimed value of P_{r_{d}', r_{d}, i} using its definition.
To sum it up, we reduced a claim on V_{d} to two claims on V_{d-1}.
Intermediate rounds
We could keep going like this down the first layer. However, this would mean evaluating V_0 at 2^d points. This exponential blow up would make the protocol impractical. Thankfully, there are two standard tricks we can use in order to avoid this problem. Those are largely discussed and explained in the Hyrax and Libra paper.
- The original GKR paper asks the prover to send the univariate restriction of V_i to the line going through v_{0, i} and v_{1, i} and use a random point on this line as the next evaluation point.
- An alternative approach due to Chiesa et al. is to run a modified sumcheck over a random linear combination \mu_0 P_{q', q_0, i} + \mu_1 P_{q', q_1, i}. By doing this, we reduce the problem of evaluating V_i at two points to evaluating V_{i-1} at two point. It is modified in the sense that the “circuit geometry functions” add_i and mul_i are modified from round to round:
\begin{array}{l}(\mu_0 P_{q', q_0, i} + \mu_1 P_{q', q_1, i})(h', h_L, h_R) \\ \quad= eq(q', h')\cdot \left[\begin{array}{c}(\mu_0add_i(q_0, h_L, h_R)+\mu_1add_i(q_1, h_L, h_R))\cdot(V_{i-1}(h', h_L)+V_{i-1}(h', h_R)) \\[1mm]+ (\mu_0mul_i(q_0, h_L, h_R)+\mu_1mul_i(q_1, h_L, h_R))\cdot V_{i-1}(h', h_L)\cdot V_{i-1}(h', h_R)\end{array}\right]\end{array} The overhead of this method is negligible.
Hyrax and Libra suggest to use the trick (2) for the intermediate steps. For the last rounds, we will instead apply the trick (1). This is to ensure that the verifier evaluates only one point of V_0.
The last steps
At the final steps, the verifier evaluates V_0 at the point output by the last sumcheck.
Cost analysis
As a sum up the verifier:
- Generate the first randomness by hashing (x, y). One (|x| + |y|)-sized hash. In practice, this computation is larger than all the individual hashes. We expand later on a strategy making this practical.
- Evaluates V_{d} and V_0 at one point each.
- d(2b_G + b_N) consistency checks. As a reminder they consists in evaluating a low-degree polynomial at 3 points: 0, 1, \eta. And calling a random oracle.
For the prover
- Evaluate the V_k. This is equivalent to execute the computation.
- Compute the polynomials of the sumcheck: ~\alpha dNG + \alpha dGb_G multiplications, where \alpha is small (~20). Since, in practice N \gg b_G, we can retains 20dNG.
- d(2b_G + b_N) fiat-shamir hashes to compute