ZKMPC: Publicly Auditable MPC for general-purpose computations

Cryptography Multiparty Computation
1

TL;DR

  • We extended the MPC protocol SPDZ to create a publicly auditable version that enables third-party verification of input constraints and calculation results.
  • SPDZ is well-suited for arithmetic operations but less effective for bitwise operations. We now support both types of computations, along with comparisons and conditional branching, broadening the range of possible applications.
  • As an example, we implemented a Game Master (GM)-free werewolf game using MPC.

1. Introduction

Our project enables third-party verification of the correctness of MPC computation results.

Multi-Party Computation (MPC) is a protocol that allows multiple parties to perform computations on their secret inputs without revealing those inputs to others. For instance, the SPDZ protocol [1] facilitates secure computations even in the presence of malicious actors.

“Publicly auditable MPC” is a concept that refers to an MPC system where the results of computations can be verified by a third party. We have developed “ZKMPC,” an extension of SPDZ-based publicly auditable MPC (PA-MPC), tailored for scenarios where specific constraints are placed on the input values.

Some of the computations and circuits we aim to support with MPC extend beyond simple arithmetic—they include binary-oriented operations like comparisons, bit decomposition, and more. Adding support for these operations significantly broadens the range of calculations that MPC can handle. For example, efficient calculations involving Pedersen commitments require a bit-decomposition step to break down the exponential component into separate powers for further combination.

The objective of this project is to create a general-purpose PA-MPC with potential applications in blockchain technology.

The code for this project can be found here.

This project has received funding from the PSE Grants Program and is a continuation of the previous topic.

2. Background

2.1 What is MPC?

Multi-Party Computation (MPC) allows multiple parties to compute a function over their private inputs without revealing those inputs to each other. It ensures privacy while enabling collaborative computations.

For example, the SPDZ protocol is an MPC protocol that ensures security even against malicious adversaries. It leverages techniques such as secret sharing and homomorphic encryption to enable secure collective computations.

2.2 The Role of Zero-Knowledge Proofs and Public Auditability in MPC

Public auditability is essential in many MPC applications to ensure trust in computed results, especially when stakeholders are not directly involved in the computation. Traditional MPC protocols only allow participants to verify correctness, but in cases like regulatory compliance or decentralized systems, third-party verification is crucial for transparency.

Zero-Knowledge Proofs (ZKPs) enable this public verifiability by allowing a prover to convince a verifier that a computation was done correctly without revealing any underlying data.

3. Project Details

We extended the SPDZ protocol, which is based on additive secret sharing, to integrate zero-knowledge proofs for verifiable computations.

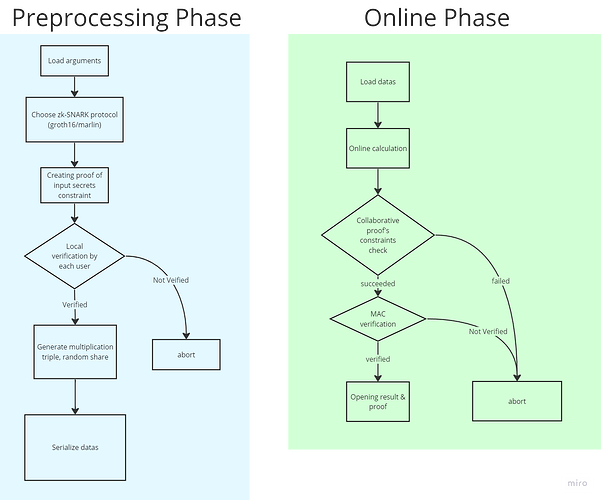
3.1 Project Architecture

project_architecture
project_architecture1371Ă—1139 83.1 KB

3.2 Technical specifications

We extend the MPC protocol called SPDZ, which is based on additive secret sharing, due to its affinity with zero-knowledge proofs, among other factors.

MPC libraries are predominantly implemented in C++, but given the increasing adoption of Rust for ZKP and blockchain projects, we chose Rust for this implementation. Rust’s safety features and growing developer community make it a strong fit for our needs.

Extension of SPDZ

We’ve implemented the above features as an extension of SPDZ.

  • We could not find any prior research on Bitwise MPC that is publicly auditable.
    • QuickSilver (using zk but not PA)
    • MPC that does not use zk
      • Yao’s Garbled Circuit (2PC)
      • BMR (MPC extension of Yao’s Garbled Circuit)
      • BGW
      • etc…
  • Good extensions from previous studies of collaborative proof.
  • Even with these updates, SPDZ retains its malicious security. In fact, the following features are achieved through a combination of MPC-secure additions and multiplications.

We referred to [3,4]. [3] proposes a protocol for primitive computation in MPC without bit-decomposition as much as possible. And [4] implies the possibility of a slightly more efficient implementation.

Modifications to arkworks library

For example, consider constraints on bit decomposition.

  • In the part that generates the R1CS constraint, the following is done:
    • Bit-decomposition operation
    • Generate constraints to ensure that the bit-decomposed value is equal to the original value
  • Contents to be implemented:
    • The bit-decomposed value was originally stored in a boolean type, so the library is modified so that it becomes a finite share.

3.3 Third-party verification of calculation and output

General MPC does not allow third-party verification of output values. A previous study that made this possible using zero-knowledge proofs is called Collaborative zk-SNARKs [2].

The output results should also be verifiable by a third party.

By adding ZKP to the MPC, the output of MPC can be publicly verified by a third party, enabling more secure and correct multi-party computation while keeping the input information confidential.

Verification of secret inputs
In many practical applications, it cannot be guaranteed that protocol participants will use appropriate input values, and there may be conditions on the input values, such as being within a specific range. In blockchain applications, it is often necessary to ensure consistency between a “pre-committed value on the chain” and the “input in MPC calculation.” To address this, ZKMPC verifies that commitments published on the blockchain match the commitments of the inputs used during MPC. This verification is facilitated by adding ZKPs to the input-sharing phase.

3.4 Supporting Bitwise Operations

Previously, ZKMPC did not support operations involving zero-knowledge circuits with bitwise operations, nor did it handle multi-party computation (MPC) for bit decomposition and comparison. Our ZKMPC now incorporates support for these critical calculations.

Specifically, we’ve implemented the following:

  • Fixed arkworks libraries with respect to R1CS
  • Fundamental bit operations (AND, OR, XOR, NOT, etc.)
  • EQZ (equality zero test)
  • Bit decomposition
  • Comparison
  • Conditional branching (IF) functions

We implemented these functions based on [Nishide, Ohta, 2007]. This research pointed out that bit decomposition itself is a rather heavy computation, and an efficient method is proposed to perform functions such as EQZ and comparison without directly using bit decomposition.

  • Equality zero (computation of [x==0])

  • Bit Decomposition ([a]_p to [a]_B)

    • Overview:
      • a is an integer from 0 to p-1
      • Generate [r] randomly.
      • Reveal [a-r].
      • Calculate the bit decomposition of [a-r], paying special attention to carry-over.
      • Let [a]_B=[r]_B+[a-r]_B
    • Details:
      • Here, p represents the modulus of the field, and l is the bit length of p.
      • simplified bit-decomposition

  • Comparison ([a<b] calculation)

    • Overview:
      • Compute [a<p/2], [b<p/2], [a-b < p/2] by interval test, where p is the modulus.
      • An interval test is a function that securely determines if a shared value is less than a constant, and outputs a shared true or false value.
      • Since the interval test involves comparing a shared value to a constant, it is more efficient than comparing two shared values.
    • Details:
      upload_6fca0a521763f0c1f3ae4b9258d25089
      upload_6fca0a521763f0c1f3ae4b9258d250891920Ă—591 81.2 KB

  • Conditional Branching (IF) Function

    • \mathrm{IF}([a], [b], [c])
      • Returns [b] when [a] is non-zero, returns [c] when [a] is zero
      • \mathrm{IF}([a], [b], [c])=[b]+([c]-[b])*[a==0]

3.5 Others

Preprocessing in MPC

In the context of ZKMPC, we extended the preprocessing phase by adding constraints to ensure guarantees on secret inputs. This preprocessing includes the generation of zero-knowledge proofs alongside traditional SPDZ preprocessing elements. Specifically, the preprocessing includes:

  • Multiplication Triples: Pre-computed shares that facilitate efficient secure multiplications during the online phase.
  • Correlated Randomness: Used to ensure that operations such as addition, multiplication, and comparison can be executed without additional interaction.
  • Zero-Knowledge Proof Setup: Preparing the cryptographic material needed to provide zero-knowledge proofs for correctness and constraints on secret inputs.
  • Commitment Scheme Preparation: Preprocessing also involves setting up Pedersen commitments to ensure that inputs remain consistent between the preprocessing and online phases.

By adding these preprocessing constraints, we provide stronger guarantees regarding secret inputs, enhancing both security and efficiency during the online phase.

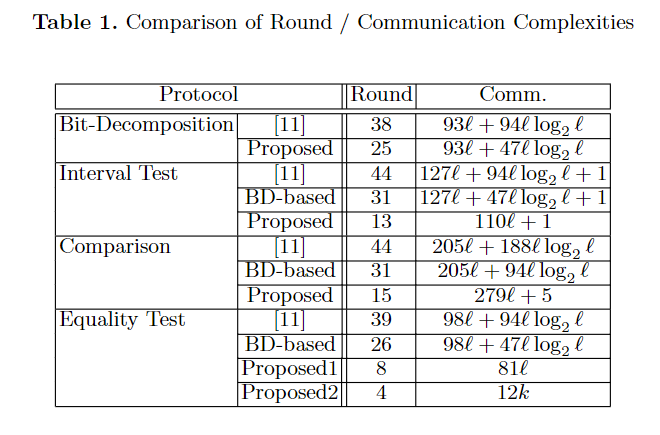
3.6 Cost Analysis

The cost analysis is based on the paper, [3] (Table 1), where l is the bit length of a modulus of the finite field.

“Round” refers to the number of times communication takes place (i.e., the number of times multiplication is invoked), and “Comm” is the communication complexity (i.e., the amount of data exchanged during communication).

We adopt the proposed implementation shown in Table 1, which achieves fewer rounds of MPC and less communication complexity than a primitive implementation using bit decomposition (BD-based).

cost analysis

4. Example: Implementation of Game Master-Free Werewolf Game Components

4.1 Overview

We will demonstrate the application of ZKMPC by implementing a version of the Werewolf game that operates without a Game Master.

The components are as follows:

  • Generating the Fortune Teller’s Public Key
  • Divination (Fortune-telling)
  • Anonymous Voting
  • Winning Judgment
  • Role Assignment

4.2 Why the Werewolf Game?

The Werewolf game is a particularly well-suited example for several reasons:

  • It incorporates several operations, including bitwise operations, that require confidential inputs from multiple participants. Removing the need for a Game Master (GM) demonstrates the strength of MPC in handling complex, decentralized interactions without a trusted authority. These operations have potential real-world applications beyond gaming.
  • The game involves a moderate level of complexity.
    • Only certain participants know the results of specific calculations, adding an element of secrecy.
    • The roles of the participants vary, contributing to dynamic gameplay.
  • This implementation is innovative as there is no existing precedent for a Game Master-free version of the game.

4.3 Technical Details

In this section, we explain how they can be expressed as mathematical formulas. We can make ZKP circuits based on these expressions.

Circuit 1: Generating the Fortune Teller’s Public Key

For each participant who is a fortune teller, a public key and a private key associated with that person are needed. Therefore, the key pair is first generated, and then MPC is performed by the participants to disclose the public key without revealing who the public key belongs to.

  1. A fortune teller generates a secret key sk and corresponding public key pk locally.
  2. Each participant calculates the following by MPC, with F_i indicating whether one is a fortune teller, and pk_i being an input (fortune teller: public key generated in step 1, others: any value):

The constraint is:

\sum_{i=1}^n F_i pk_i
  • The condition for F_i is that it should be consistent with the commitment of the position.

Circuit 2: Divination (Fortune-telling)

Using whether player i is a Werewolf (W_i \in {0,1}) and whether the fortune teller wants to know the result for player i (C_i \in {0,1}, all but one are 0), whether player i is a werewolf (=1) or not (=0) is calculated by

\sum_{i=1}^{n} W_i C_i

W_i and C_i are distributed to each player as shares, and the final result is encrypted so that only the fortune teller can see it.

At this time:

  • The condition regarding C_i is that C_i should be 1 for only one value of i, and 0 for all other values.
  • The condition for W_i is that it should be consistent with the commitment of the position.

Circuit 3: Anonymous Voting (Determination of Who Gets the Most Votes)

  • Naive idea:
    • It can be expressed as “the number of votes cast for a player is greater than or equal to the number of votes cast for all other players.”
  • The formula for determining the maximum voter is as follows:
    b_i=\prod_{j=1}^n \mathrm{GTE}(a_i, a_j)
    • b_i: 1 when player i has the most votes, 0 otherwise
    • a_i: Number of votes cast for player i.
    • \mathrm{GTE}(x,y): (Abbreviation for Greater Than or Equal). 1 when x \geq y, 0 otherwise.

Circuit 4: Winning Judgment

  • Naive idea:
    • It can be expressed as “if the number of werewolves \geq the number of villagers, the wolves win”, “if the number of werewolves = 0, the villagers win”, or “if 1 \leq the number of werewolves < the number of villagers, the game continues”.
  • The formula for determining the victory of a game is, for example, as follows:
    \begin{aligned} f =&IF(\\ &&&N_w,\\ &&&IF(LT(N_w, N_v),3,1) ,\\ &&&2\\ &) \end{aligned}
    • f: game state, 1 when the wolves win, 2 when the villagers win, 3 when the game continues
    • N_w: Number of living werewolves
    • N_v: Number of living villagers
    • \mathrm{EQZ}(x): (Abbreviation for Equal Zero). 1 when x=0, 0 otherwise.
    • \mathrm{LT}(x,y): (Abbreviation for Less Than). 1 when x < y, 0 otherwise.

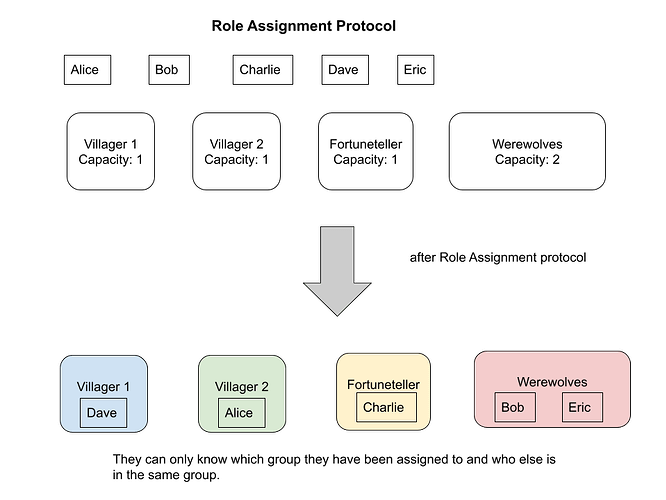
Circuit 5: Role Assignment

  • Concept:
    • Each participant makes a random substitution, and the grouping protocol is implemented by MPC.
  • Requirement:
    • We would like to assign a position randomly and disclose it only to the player themselves.
    • For a specific position, such as werewolf, we want to know which members belong to the group.
    • We want to create a commitment for each member’s position and make it publicly auditable.

the_role_assignment_protocol_diagram
the_role_assignment_protocol_diagram960Ă—720 46.9 KB

  • For grouping protocols:
    • ref. [5]
    • ZKMPC creates the following proof:
      • Public parameter
        • n: number of participants
        • m: number of groups
        • \tau: substitution matrix of a particular type of order
      • Witness
        • M_i (i\in \{1,\dots, n\}): shuffle matrix of player i
        • r_i: randomness of player i
      • Instance
        • Commitment c_i
      • Constraint
        • M_i for each i is a substitution matrix
        • For each M_i, the submatrix consisting of rows n+1 to n+m and columns n+1 to n+m forms an identity matrix.
        • \rho = M^{-1}\tau M where M=\prod_{i=1}^n M_i
        • For each j, \rho^{i}(j) = x_{i,j}
        • Where x_i is the group number contained in x_{i,j}
        • For each i, c_i = Commitment(x_i, r_i)
      • Third-party verification is done by including the commitment c_i = Commitment(x_i, r_i) in the proof
    • Compute the following in MPC:
      • Input:
        • [M_i]: Shuffle matrix of player i.
        • (1, \dots, n): Constant number vec from 1 to n.
      • Output:
        • [x_i] = ([x_{i,1}], \dots, [x_{i,n}]): a shuffled shared vector representing each user’s group membership, including both the group that the i-th user belongs to and their fellow members within that group.
    • Reveal [x_i] to player i.
      • Player i now knows their role.
    • Player i commits x_i, where r_i is randomness
      • c_i = Commitment(x_i, r_i)

5. Benchmark

256-bit field is used in the ZKMPC benchmark below.

5.1 Online Phase

run_online.zsh (Marlin): 7s

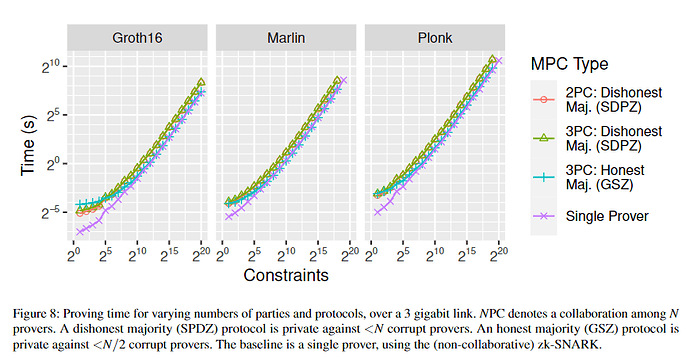
Since the proving and verifying times of circuits depend on the number of constraints, and the dependency is roughly the same as in the previous study, Collaborative zk-SNARKs, only the number of constraints will be recorded here.

For example, when the constraints \approx 2^{10} and executing in Marlin, the proving time \approx 2 s as follows.

relation_of_constraints_and_proving_time
relation_of_constraints_and_proving_time870Ă—452 66.8 KB

cited from [2].

5.2 MPC Calculation: Bitwise Operation Components

Calculation Name Total Time Communications Content
EqualityZeroTest 211ms ~ 226ms 3,795 Input: 1 field element. Output: is zero value
BitDecomposition 479ms ~ 652ms 8,337 Input: 1 field element. Output: bitwise share.
LessThan 1.092s ~ 1.178s 20,529 Input: 2 field elements. Output: comparison result value

Where communications refer to the number of broadcasts in the protocols.

5.3 Circuits Constraints: Main Circuits 1

Circuit Name Total Constraints Content
MySecretInputCircuit 6,574 1 secret & its Pedersen commitment & additional range constraints
PedersenComCircuit 2,544 1 secret & its Pedersen commitment
MyCircuit 5,094 2 committed secrets & their multiplication

5.4 Circuits Constraints: Main Circuits 2 (MPC Bitwise Operations)

Circuit Name Total Constraints Proving Time Content
BitDecompositionCircuit 672 2.028s 1 secret
SmallerEqThanCircuit 621~625 1.468s~1.483s 1 bitwise secret & 1 comparison
EqualityZeroCircuit 4 368.426ms 1 secret
PedersenComCircuit 2,543 6.572s 1 secret & its Pedersen commitment
SmallerThanCircuit 2,016 4.039s 2 secrets and ordering

5.5 Circuits Constraints: Werewolf’s Circuits

Circuit Name Total Constraints Content
KeyPublicizeCircuit (3 parties) 15,266 3 committed secrets & their sum
DivinationCircuit (3 parties) 22,249 Many committed secrets & ElGamal encryption
AnnonymousVotingCircuit (3 parties) 8,065 3 committed secrets & some bit operations
WinningJudgementCircuit (3 parties) 9,648 3 committed secrets & some bit operations
RoleAssignmentCircuit (3 parties) about 65,644 3 committed secrets & grouping protocol

6. Impact

If third-party verification becomes possible in multiparty computation, it can be applied to blockchain.

If collaborative proof can be created, including bitwise operations, the versatility of ZKMPC will increase and it can be used in a wider range of situations. In addition, secret computation in two or three parties has a wide range of applications. Recently, re-staking techniques such as EigenLayer have been developed, and ZKMPC may be able to efficiently perform re-staking while ensuring security in such situations. In addition, in the convolution layer of machine learning, linear and nonlinear operations are mixed, and it is important to be able to convert between the two. This will be a pioneering example of such a case.

7. Future Issues

  • Computational cost
    • Since the number of constraints in the circuit to verify PedersenCommitment is about 7000, it is expected that the proof time will increase by 1 to 10 seconds even if we increase the number of committed inputs by one.

Bibliography

3 Likes