1. Project Overview
1.1 Overview
Multi-Party Computation (MPC) allows protocol participants to collaborate without exposing their own private input values to other participants.
This project extends one of the MPC protocols, SPDZ [1], and adding following functionalities:
- Proof that the input values satisfy the conditions when there are restrictions on the input values of the protocol participants
- Third-party verification that the MPC calculation results are correct
The SPDZ is an extension of SPDZ [1] that enables third-party verification of the correctness of calculation results by the MPC.
The objective of this project is to achieve part of the goal of using more secure general purpose MPCs on the blockchain.
Our code is here.
This project has received funding from the PSE Grants Program.
1.2 Project Detatils
This project aims to use zero-knowledge proofs to extend an MPC protocol called SPDZ to allow third-party verification of the constraints on secret input values and the correctness of output values.
Third-party verification of calculation and output
General MPC does not allow third-party verification of output values. A previous study that made this possible using zero-knowledge proofs is called Collaborative zk-SNARKs [2].
The output results should also be verifiable by a third party.
By adding ZKP to the MPC, the output of MPC can be publicly verified by a third party, enabling more secure and correct multi-party computation while keeping the input information confidential.
Verification of secret inputs
Given the actual implementation of MPC, it cannot be guaranteed that protocol participants will put in appropriate values as input values. There may also be situations where conditions are imposed on the input value, such as below a certain value or one of several candidates.
When considering the application of MPC to the blockcahin, the consistency of “Pre-commited value on the chain” and “Input in MPC calculation” must be verified. So we impose that they are conicide, which the commitment publicized on chain in preprocessing phase and the commitment of the input in online phase.
Considering such a situation, we propose and implement an extension protocol of MPC that allows the private input of protocol participants to be verified using zkp.
Technical specifications
We extend the MPC protocol called SPDZ, which is based on additive secret sharing, in view of its affinity with zero-knowledge proofs, etc.
MPC libraries are mostly C++ -based, but given that many ZKP and Blockchain-related projects are Rust implementations, we will implement this project in Rust.
This project will include:
- Local simulation of SPDZ including zero-knowledge proofs
- The ability to use zero-knowledge proofs to prove that private input values are correctly passed on to other participants as shares
- An implementation of some of the computations in a werewolf game as an application example
2. Structure
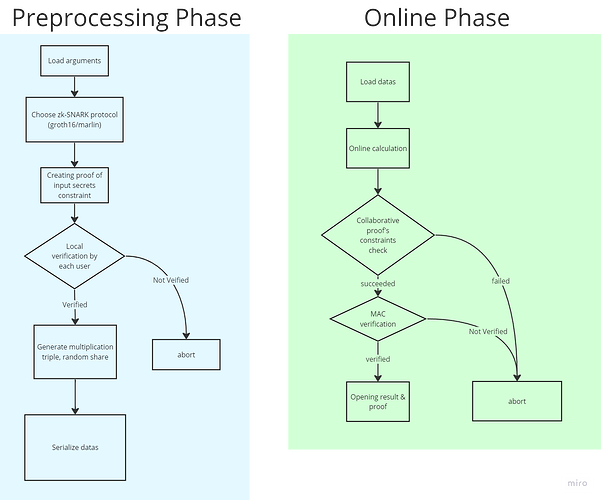
2.1 Preprocessing Part+ZKP to prove that SPDZ shares are correctly made for conditional secret inputs.
In the preprocessing phase of SPDZ, shares of secret inputs are created. In situations where the secret input is constrained, we use ZKP to prove that the share is correctly created from the secret input that satisfies the constraint.
In this project, ZKP generation for input constraints is performed outside the MPC (SPDZ) protocol.
The constraints on private inputs can be specified, such as they must be a boolean value, they must be in this range, etc. In any case, each party can abort if the input constraints are not satisfied.
Compared to doing so inside the MPC, it allows participants to immediately verify the validity of a given share. In addition, while SPDZ only supports additive and multiplicative methods, it allows for verification regarding complex constraints. Thus, the advantage is that the same method can be applied universally to a variety of MPCs.
However, there is a drawback that it is difficult to consolidate ZKP for input constraints and ZKP for MPC calculation into one ZKP. Therefore, it is necessary to broadcast the commitment of the input and verify the entire MPC through it.
Technical Details
The additive secret sharing method is used in SPDZ, and the secret information S is kept in the form of shares S_i such that S=\sum_{i=1}^nS_i.
With respect to the input values of SPDZ, a participant’s share of secret information X is constructed as follows.
- Each participant has a share r_i of a random number r. The value of r is unknown to anyone at this point.
- The participant who wants to create a share of secret information x recovers the value of r and broadcasts \varepsilon=x-r.
- Each participant P_i determines its share x_i of x as x_1=r_1+\varepsilon, x_i=r_i(i\neq 1). In this case, x=\sum x_i holds.
The share x_i is created by such a procedure, but it is not generally known whether each participant has composed the share according to the protocol, or whether the original secret information x satisfies certain conditions.
Therefore, for each conditional secret input x, we use zkp to prove that each person’s share of x has been correctly created.
- Secret input
- x: secret information
- Randomness: Randomness used in a commitment of x.
- Public input
- \mathrm{Param}_{pedersen} : Parameters of Pedersen commitment.
- h_x: commitment of secret value x by randomness Randomeness.
- (optional): variables apperead in \mathrm{Constraint}(\cdot)
For these, the participant who has secret inputs creates a proof so that the following relation is satisfied.
where the \mathrm{Constraint}(\cdot) is the condition that x must satisfy.
2.2 Online Part
Implement the zkp created in Milestone 1 in SPDZ so that MPC calculations can be performed with proofs regarding the input. This enables third-party verification that the secret input to the MPC protocol correctly meets the conditions and is distributed as a share.
Then, the online phase of the SPDZ will be implemented. Together with the pre-processing part that was implemented in Milestone 1, the implementation of the SPDZ will be completed.
To make the entire SPDZ compatible with Collaborative proof, the implementation in Collaborative zk-SNARKs will be implemented in a more user-friendly form with reference to the implementation in Collaborative zk-SNARKs. By combining these, the calculation and output value parts can also be verified by a third party.
3. Example: Werewolf game
One of the use cases we are considering for our project is a werewolf game. Since werewolf games require values tied to individual identities as MPC input, input constraints such as this one need to be checked in advance and made a commitment.
This section implements an example calculation for obtaining the fortune-telling result of a fortune-teller in the Werewolf game. The divination result is encrypted so that only the diviner can obtain it.
Technical Details
In order to implement the use of abilities of werewolf game role using zk-mpc, we required public key cryptography. We used the ElGamal cryptography for this implementation.
Note that although we did not specify the method of assigning role this time, we impose the constrains that only the fortuneteller can input meaningful public key and that W_i must be consistent with the role variable used in the following as a constraint during the commitment.
Cirucit 1: Generating Fortune teller’s public key
For each participant who is a fortuneteller, a public key and a private key associated with that person are needed. Therefore, the key pair is first generated, and then mpc is performed by the participants to disclose the public key without revealing who the public key belongs to.
- A fortune teller generates a secret key sk and correspoindg public key pk in local.
- Each participant calculates the following by MPC with F_i is whether one is a fortune teller, pk_i is a input (fortune teller: public key generated step1, others: any value)
The Constraint is
- The condition for F_i is that it should be consistent with the commitment of the position.
Circuit 2: Divination
Using whether player i is a Werewolf (W_i \in \{0,1\}) and whether the fortuneteller wants to know the result of player i (C_i \in \{0,1\} , all but one are 0), whether player i is a werewolf (=1) or not (=0) is calculated by
W_i and C_i are distributed to each player as a share, and the final result is encrypted so that only the fortuneteller player can see it.
At this time,
- The condition regarding C_i is that C_i should be 1 for only one value of i, and 0 for all other values.
- The condition for W_i is that it should be consistent with the commitment of the position.
4. Benchmark
Preprocessing phase
Groth16: 1.5s
Marlin: 10s
Online phase
run_online.zsh(Marlin): 7s
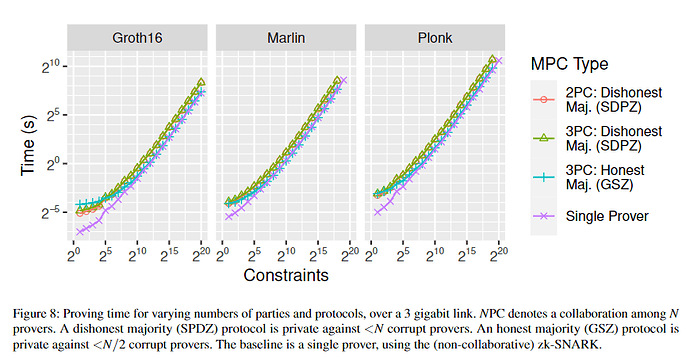
Since proving and verifying time of ciruits are depends on the number of constrains, and the way it depends is roughly the same as in the previous study, Collaboative zk-SNARKs, only the number of constrains will be recorded here.
For example, when the constraints \approx 2^{10} and executing in Marlin, then the Proving time $\approx 2$s as follows.
cited from [2].
Our Main Circuits are:
| Circuit Name | Total Constrarints | Content |
|---|---|---|
| MySecretInputCircuit | 6574 | 1 secret & its Pedersen commitment & additional range constraints |
| (PedersenComCircuit) | 2544 | 1 secret & its Pedernsen commitment |
| MyCircuit | 5094 | 2 commited secrets & their multiplication |
Werewolf’s circuits are:
| Circuit Name | Total Constrarints | Content |
|---|---|---|
| KeyPublicizeCircuit (3 parties) | 15266 | 3 commited secrets & their sum |
| DivinationCircuit (3 parties) | 22249 | many commited secrets & ElGamal encryption |
5. Future issues
- Computational cost
- Since the number of constraints in the circuit to verify PedersenCommitment is about 7000, it is expected that the proof time will increase by 1 to 10 seconds even if we increase the number of inputs by one.
- share-conversion
- In the current implementation, operations involving Boolean are not very efficient.
6. Impact
The combination of MPC and ZKP has been tooled to provide a mechanism for third-party verification of input and output values in a way that is easy to use widely.
This is also the first attempt to implement MPC in such a way as to prove that the MPC input values satisfy certain conditions.
The impact of this project extends beyond secure data encryption and privacy-preserving computation. By leveraging the properties of MPC and Zero-Knowledge Proofs, the project opens up possibilities for various use cases, including those enabled by blockchain technology.
Bibliography
- [1] SPDZ original paper
- title: Multiparty Computation from Somewhat Homomorphic Encryption
- Multiparty Computation from Somewhat Homomorphic Encryption
- [2] Collaborative zk-SNARKs
- title: Experimenting with Collaborative zk-SNARKs: Zero-Knowledge Proofs for Distributed Secrets
- Experimenting with Collaborative zk-SNARKs: Zero-Knowledge Proofs for Distributed Secrets