Authors: Joachim Neu, Ertem Nusret Tas, David Tse
This attack was subsequently published in: “Two More Attacks on Proof-of-Stake GHOST/Ethereum”
TL;DR: Proposal weights were suggested and implemented to mitigate earlier balancing attacks. We show that the LMD aspect of PoS Ethereum’s fork choice enables balancing attacks even with proposal weights. This is particularly dire because PoS GHOST without LMD is susceptible to the avalanche attack.
We assume basic familiarity with the beacon chain fork choice specification (cf. Gasper), earlier balancing attacks, and the idea of proposal weights.
Preliminaries
Recall the following from earlier discussions:
- On a high level, the balancing attack consists of two steps: First, adversarial block proposers initiate two competing chains—let us call them Left and Right. Then, a handful of adversarial votes per slot, released under particular circumstances, suffice to steer honest validators’ votes so as to keep the system in a tie between the two chains and consequently stall consensus.
- It is quite feasible for an adversary to release two messages to the network in such a way that roughly half of the honest validators receive one message first and the other half of the honest validators receives the other message first. Certainly in networks with bounded adversarial delay but also in networks with random delay.
- Here is how the LMD (Latest Message Driven) rule deals with equivocating votes. Under LMD, every validator keeps a table of the ‘latest message’ (here, message = vote) received from each other validator, in the following manner: when a valid vote from a validator is received, then the ‘latest message’ table entry for that validator is updated if and only if the new vote is from a slot strictly later than the current ‘latest message’ table entry. Thus, if a validator observes two equivocating votes from the same validator for the same time slot, the validator considers the vote received earlier in time.
High Level
The LMD rule gives the adversary a remarkable power in a balancing attack: Once the adversary has set up two competing chains, it can equivocate on them. The release of these equivocating votes can be timed such that the vote for Left is received by half of honest validators first, and the vote for Right is received by the other half of honest validators first. Honest validators are split in their views concerning the ‘latest messages’ from adversarial validators. Even though all validators will soon have received both votes, the split view persists for a considerable time due to the LMD rule (and since the adversarial validators release no votes for later slots).
As a result, half of the honest validators will see Left as leading, and will vote for it; half will see Right as leading, and will vote for it. But since honest validators are split roughly in half, their votes balance, and they continue to see their respective chain as leading. (The adversary might have to release a few votes every now and then to counteract any drift stemming from an imbalance in which chain honest validators see as leading.) This effect is so stark, that it could only be overcome using proposer boosting if the proposal weight exceeded the adversarial equivocating votes (which is some fraction of the committee size) by more than a constant factor (else if the adversary leads that constant factor number of slots, it can surpass the proposer boost again). In that case, the proposer effectively overpowers the committees by far, thus eliminating the purpose of committees.
A Simple Example
Let W=100 denote the total number of validators per slot. Suppose the proposal weight is W_p=0.7 W = 70, and the fraction of adversarial validators is \beta=0.2. Furthermore, for simplicity, assume that the attack starts when there are five consecutive slots with adversarial leaders.
During the first four slots, the adversary creates two parallel chains Left and Right of 4 blocks each, which are initially kept private from the honest validators. Each block is voted on by the 20 adversarial validators from its slot. Thus, there are equivocating votes for the conflicting blocks proposed at the same slot. For the fifth slot, the adversary includes all equivocating votes for the Left chain into a block and attaches it on the Left chain; and all the equivocating votes for the Right chain into an equivocating block and attaches it on the Right chain.
With this, votes are “batched” in the following sense. The adversary releases the two equivocating blocks from the fifth slot in such a way that roughly half of the honest validators see the Left block first (call H_{\mathrm{Left}} that set of honest validators) and with it all the equivocating votes for the Left chain; and half of the honest validators see the Right block first (call H_{\mathrm{Right}} that set of honest validators) and with it all the equivocating votes for the Right chain. (Note that this trick is not needed in networks with adversarial delay, where the release of equivocating votes can be targeted such that each honest validator either sees all Left votes first or all Right votes first.)
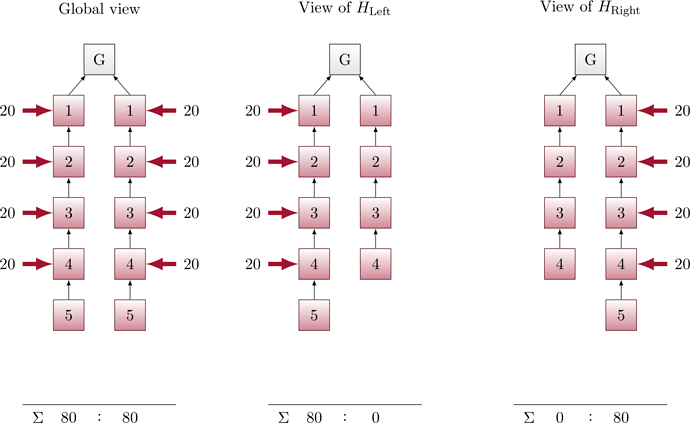
Figure 1:
By the LMD rule, validators in H_{\mathrm{Left}} and H_{\mathrm{Right}} believe that Left and Right have 80 votes, respectively. They also believe that the respective other chain has 0 votes (as the later arriving votes are not considered due to LMD).
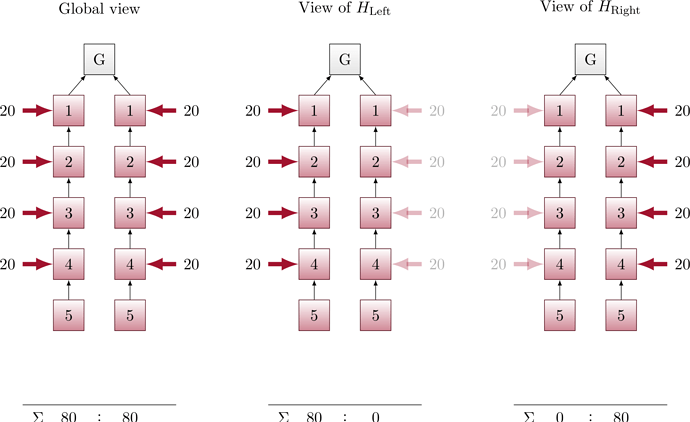
Figure 2:
Now suppose the validator of slot 6 is honest and from set H_{\mathrm{Left}}. Then, it proposes a block extending Left. Left gains a proposal boost equivalent to 70 votes.
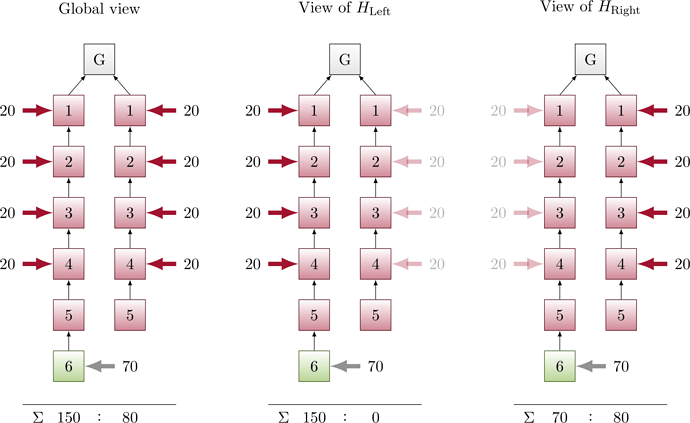
Figure 3:
Thus, validators in H_{\mathrm{Left}} see Left as leading with 150 votes and vote for it. Validators in H_{\mathrm{Right}} see Left has 70 votes while Right has 80 votes, so they vote for Right. As a result, their vote is tied—Left increases by roughly half of honest votes and Right increases by roughly half of honest votes.
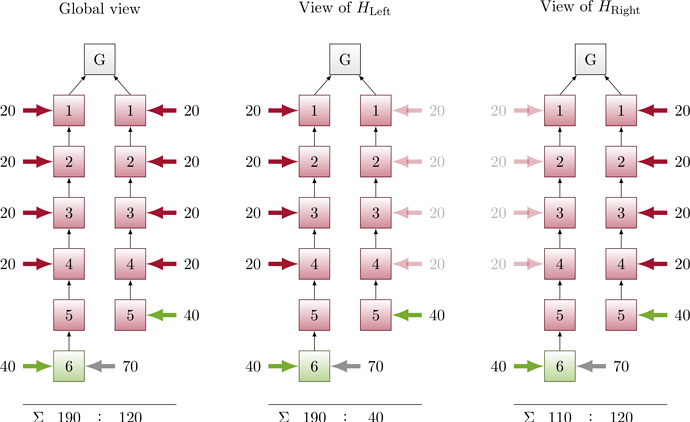
Figure 4:
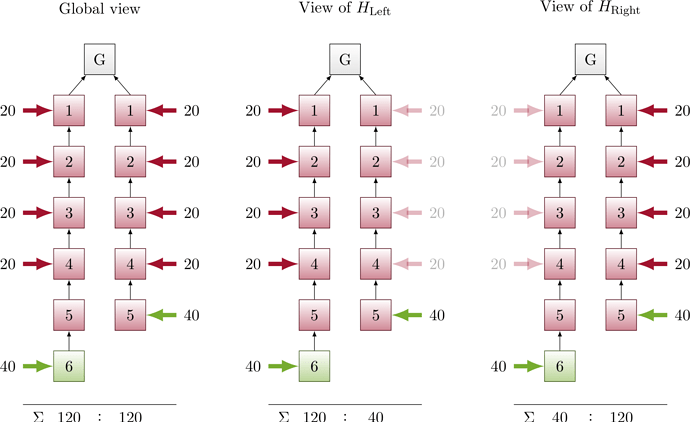
At the end of the slot, the proposer boost disappears. In the view of each honest validator, both chains gained roughly the same amount of votes, namely half of the honest validators’ votes. Assuming a perfect split of |H_{\mathrm{Left}}|=|H_{\mathrm{Right}}|=40, Left:Right is now 120:40 in the view of H_{\mathrm{Left}} and 40:120 in the view of H_{\mathrm{Right}} (up from 80:0 and 0:80, respectively).
Figure 5:
Thus, this pattern repeats in subsequent slots, with the honest validators in H_{\mathrm{Left}} and H_{\mathrm{Right}} solely voting for the chains Left and Right, respectively, thus maintaining a balance of weights (in global view—in the LMD view of each validator, they keep voting for the chain they see leading, and “cannot understand” why other honest validators keep voting for the other chain) and perpetuating the adversarially induced split view.