We thank Yan X. Zhang, Danny Ryan and Vitalik Buterin for review and discussions.
This attack was subsequently published in: “Ebb-and-Flow Protocols: A Resolution of the Availability-Finality Dilemma”
Gasper is the current proposal for Eth2’s beacon chain. In this post, we summarize a liveness attack against Gasper in the synchronous network model. We have recently presented this attack in this manuscript, and details can be found in Section II and Appendix A of that manuscript. Python code for a high-level simulation of the attack can be found here. Check out the code for even more details on how exactly adversarial and honest validators behave in each stage of the attack. The goal of this post is to provide an easy-to-understand explanation of the attack with step-by-step illustrations, so that the attack is accessible for a broad audience and the community can be on the watch for similar issues as they may arise in other contexts.
Severity of the attack
Before we discuss the attack, a few words to put it in context.
To be able to compare the security guarantees provided by different consensus protocols, the consensus literature usually benchmarks protocols under standard network models. Arguably the most basic model is that of a synchronous network, where the adversary can decide for each network message how long to delay its delivery, up to a maximum delay bound \Delta. Note that the synchronous model does not allow for network partitions or any other periods of asynchrony in which the maximum network delay could temporarily exceed \Delta. Another standard model that captures such periods of asynchrony is that of a partially (or eventually) synchronous network, where before an adversarially chosen global stabilization time \mathsf{GST} the adversary can delay network messages arbitrarily, while after \mathsf{GST} the adversary can delay messages only up to a maximum delay bound \Delta. Thus, before \mathsf{GST}, the network undergoes a period of asynchrony or network partition, and with \mathsf{GST} the network returns to its normal synchronous operation.
It is perhaps not surprising that consensus is easier in synchronous networks and harder in partially synchronous networks. (Note that synchronous networks are a special case of partially synchronous networks, with \mathsf{GST} = 0.) Indeed, there are provably secure consensus protocols for synchronous networks that tolerate up to 50\% adversarial validators, while provably secure consensus protocols for partially synchronous networks only tolerate up to 33\% adversarial validators. For a pedagogical example, check out Streamlet.
For our attack, we assume that an adversary has the following capabilities:
A) The adversary knows at what points in time honest validators execute the Gasper fork choice rule \mathsf{HLMD}(G) (see Algorithm 4.2 of Gasper).
B) The adversary is able to target a message (such as a proposed block or a vote) for delivery to an honest validator just before a certain point in time.
C) Honest validators cannot update each other arbitrarily quickly about messages they have just received.
Note that A) is given by design of Gasper which has predetermined points in time at which honest validators are supposed to cast their votes. Conditions B) and C) are satisfied in the two standard consensus-theoretic models we have discussed before, because the adversary can deliver its own messages without delay (providing B)) and it can delay messages exchanged between honest validators (providing C)). As a result, we can already conclude that Gasper is not secure even in the basic synchronous network model, and thus also not in the partially synchronous model (where the adversary is strictly more powerful).
It is up to everyone to judge for themselves whether they think an adversary might have the above capabilities in a global consensus mechanism such as Ethereum running over the Internet. Some might perhaps argue that it is unrealistic that the adversary has power over network message delays, as is assumed in standard models.
To this we remark threefold:
- Since we do not know what exact capabilities an adversary might have, why not err on the side of caution and design protocols for pessimistic worst-case scenarios?
- In particular since we have protocols that are secure even under these pessimistic scenarios, why settle for anything short of that?
- Finally, any real system will have plenty of ‘imperfections’ which bring even more uncertainty about the adversary’s capabilities. For instance, network communication is neither point-to-point nor broadcast but a peer-to-peer gossip network – what additional influence over the message delay might this provide for the adversary? Some of such imperfections can be lumped into a pessimistic worst-case model.
Personally, we think that protocols should be evaluated in standard consensus-theoretic models (such as under synchrony or partial synchrony) to avoid making overly specific assumptions about the adversary’s capabilities and running the risk of underestimating the adversary, and to enable a fair evaluation of different protocols.
Overview of the attack
Now to the attack. Gasper is a vote-based proof-of-stake protocol which combines Casper FFG with a committee-based blockchain block proposal mechanism where the fork
is chosen using the ‘greedy heaviest observed sub-tree’ (GHOST) rule under the ‘latest message driven’ (LMD) paradigm, i.e., taking into consideration only the most recent vote per validator. A Gasper vote consists of two parts, a GHOST vote and a Casper FFG vote. While details of Gasper preclude the vanilla bouncing attack (cf. here, here, and here) on the Casper FFG layer, Gasper is vulnerable to a similar balancing attack on the GHOST layer.
Recall that Gasper is run with C slots per epoch. For simplicity, let C divide n so that every slot has a committee of size n/C. For each epoch, a random permutation of all n validators assigns validators to slots’ committees and designates a proposer per slot. Per slot, the proposer produces a new block extending the tip determined by the fork choice rule \mathsf{HLMD}(G) executed in local view G (see Algorithm 4.2 of Gasper). Then, each validator of the slot’s committee decides what block to vote for using \mathsf{HLMD}(G) in local view G.
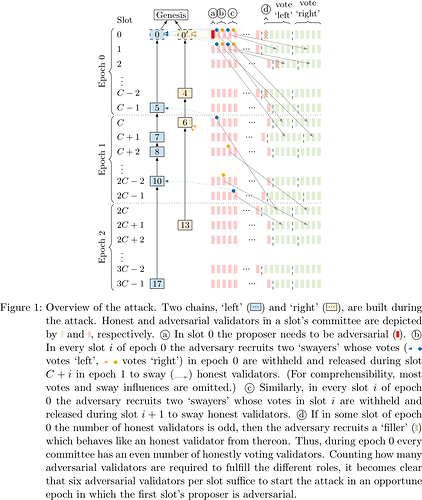
For the Casper FFG layer, a block can only become finalized if two-thirds of validators vote for it. The adversary in our attack aims to keep honest validators split between two options (‘left’ and ‘right’ chain, see Figure 1 for an overview of the attack) indefinitely, so that neither option ever gets two-thirds votes and thus no block ever gets finalized.
The basic idea of the attack is as follows (for a detailed description, see Appendix A of our manuscript). The adversary waits for an opportune epoch to kick-start the attack. An epoch is opportune if the proposer in the first slot is adversarial and there are ‘enough’ (six suffice; explained in detail in Appendix A of our manuscript) adversarial validators in every slot of the epoch. In particular in the regime of many validators (n \to \infty), the probability that a particular epoch is opportune is roughly f/n, where f is the number of adversarial validators. For ease of exposition, let epoch 0 be opportune.
The adversarial proposer of slot 0 equivocates and produces two conflicting blocks (‘left’ and ‘right’, see Figure 2) which it reveals to two suitably chosen equal-sized subsets of the committee. One subset votes ‘left’, the other subset votes ‘right’ – a tie.
The adversary then selectively releases withheld votes from slot 0 (see Figure 3) to split validators of slot 1 into two equal-sized groups, one which sees ‘left’ as leading and votes for it, and one which sees ‘right’ as leading and votes for it – still a tie.
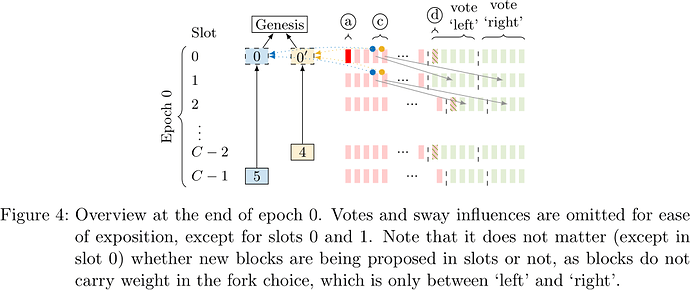
The adversary continues this strategy to maintain the tie throughout epoch 0 (see Figure 4).
During epoch 1, the adversary selectively releases additional withheld votes from epoch 0 (see Figure 5) to keep splitting validators into two groups, one of which sees ‘left’ as leading and votes ‘left’, the other sees ‘right’ as leading and votes ‘right’.
Note that these groups now do not have to be equal in size. It suffices for the adversary to release withheld votes selectively so as to reaffirm honest validators in their illusion that whatever chain they previously voted for happens to still be leading, so that they renew their vote. Due to the LMD paradigm of Gasper’s fork choice rule, only the most recent vote per validator counts. At the end of epoch 1 there are still two chains with equally many votes and thus neither gets finalized.
Finally, for epoch 2 and beyond the adversary repeats its actions of epoch 1 (see Figure 1). Note that the validators whose withheld epoch 0 votes the adversary used to sway honest validators in epoch 1 have themselves not voted in epoch 1 yet. Thus, during epoch 2 the adversary selectively releases votes from epoch 1 to maintain the tie between the two chains. This continues indefinitely.
Conclusion
Thus, Gasper is not live in the synchronous network model. In fact, all we need for this attack to succeed are the three adversary capabilities presented initially, which are used to sway honest validators via selectively releasing withheld votes. What is more, the block proposal mechanism is rendered unsafe by the attack as the chosen fork flip-flops between ‘left’ and ‘right’. Note that the probability that an epoch is opportune for the adversary to start the attack is \approx f/n (for large n), so that even an adversary controlling only 1\% of validators would have to wait on average only 100 epochs to be able to launch the attack.