Prevention of bouncing attack on FFG

[nrryuya]

TL;DR

We present a simple fix on FFG which makes it difficult for an attacker to continue bouncing attack unless the attacker has strong control over the network.

Prerequisites:

Analysis of bouncing attack on FFG

TL;DR In this post, I dig into the bouncing attack on Casper FFG, which is already known to potentially make a permanent liveness failure of FFG. I present specific cases where this attack can happen. Also, I describe how the choice of the fork-choice rule relates to this attack. Prerequisites: Casper FFG paper Background: Bouncing attack In Casper FFG, the fork-choice rule must start from the latest justified checkpoint. Alistair Stewart found that this introduces an attack vector where th…

(Definitions and notations borrowed from it)

Fix on FFG

In Casper FFG, the fork-choice rule does not start from the genesis block, but the latest justified checkpoint. (In this post we call the block from which the fork-choice rule starts start point.) Whenever a validator sees a new latest justified checkpoint, the start point changes.

We modify this so that the start point switches to a different chain only in the first k slots of every epoch. Specifically,

• When a validator see a new latest justified checkpoint and it is conflicting to the current start point,
  • if his local clock is in the first k slots, he replaces his start point with it
  • if it is not in the first k slots, he marks it as pending
• When a validator enters a new epoch, he recalculates the latest justified checkpoint for the start point from justified checkpoints he has ever seen including ones marked as pending

Here we require k is less than \mathrm{SLOTS\_PER\_EPOCH}/3 slots.
(See below for the reason.)

Security analysis

Here we describe how the above fix prevents a bouncing attack.
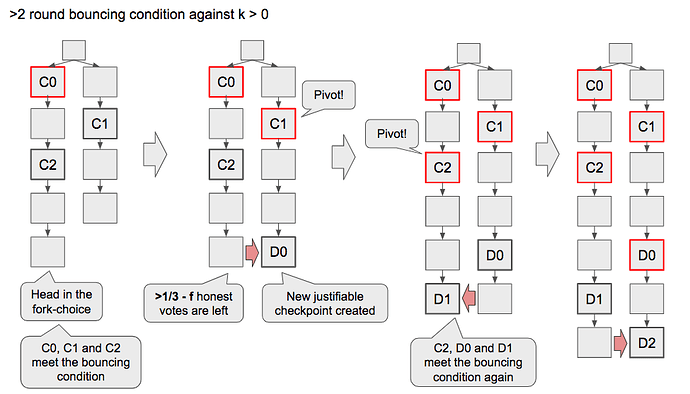
Assume at a certain time, the network becomes fully synchronous (the delay < 1 slot) and the bouncing condition is satisfied (i.e. honest validators’ start point is a checkpoint C and there is a later justifiable checkpoint C' conflicting with C ).
Let C'' be the checkpoint which the honest validators vote for in the beginning.
We argue that an attacker cannot make C'' justifiable.

In a case where there is no new latest justified checkpoint appears in the first k slots, honest validators succeed to justify C'' in this epoch.
In a case where an attacker justifies C' and publishes the votes in the first k slots, honest validators accept it as their start point. However, C'' cannot be justifiable because k < \mathrm{SLOTS\_PER\_EPOCH}/3 and hence \mathrm{FFGVotes}(C'') < n/3.

Therefore, the attacker cannot create a justifiable (but not justified) and conflicting checkpoint continuously so eventually bouncing stops when the attacker spends up all the justifiable checkpoints which are prepared before the network becomes fully synchronous.

Splitting attack

In the above argument, it is assumed that honest validators agree on whether to change their start point.
However, it is not always true because an attacker who has a strong control over the network can split honest validators; the attacker can send votes which justify C' to only a subset of the honest validators at the moment slightly before the end of k -th slot so that the recipients cannot gossip the information to other honest validators in time. By splitting, the attacker can make C'' justifiable by leaving an appropriate number of honest validators to C'' and making other validators switch to C'.

The exact condition for the attacker to make C'' justifiable is as follows.

• Let v_{C''}^H be the number of honest votes for C'' at the end of the k -th slot.
• Let x be the number of honest validators who is allocated to a slot after the first k slots and does not see C' justified in the first k slots.
• For C'' to be justifiable, x + v_{C''}^H + t \ge 2n/3 \land x + v_{C''}^H < 2n/3
  • \therefore 2n/3 - v_{C''}^H - t \le x < 2n/3 - v_{C''}^H

This is one of the “last-minute delivery” family of strategies. This strategy requires the attacker to identify at least tens of thousands of (physical) nodes with validators (public keys) and to have almost direct connections to them. It would be much more difficult than the original bouncing attack.

Therefore, our fix on FFG prevents bouncing attack under the assumption that the attacker does not always succeed in last-minute delivery. Also note that if an attacker can do last-minute delivery, he can attack on the fork-choice by splitting the votes into and keeping the balance of two chains.

Rationale

In this section, we discuss the rationale of this fix from the perspective of BFT consensus theory.

Casper FFG as locking-based pipelined-BFT

Casper FFG is one of the pipelined-BFT protocols, where the consensus consists of two phases of voting and every vote is both for the first phase (“pre-commit”) of the target checkpoint and the second phase (“commit”) of the direct parent checkpoint.
(Related works are Hotstuff and Pala.)
Also, Casper FFG adopts locking paradigm a la Tendermint in the form of slashing conditions, instead of view-change voting a la PBFT.

The difference between FFG and the other existing works is that FFG is leaderless; chain-based pre-consensus is used to create checkpoints and there is no fixed view (i.e. the checkpoint which validators can vote for) chosen by the leader of every epoch.
The advantages of this approach are (i) no security/performance loss due to leader’s failure and (ii) flexibility of the tradeoff between time to finality and number of validators.

Why “fork-choice starts from the latest justified checkpoint”?

The rule that “the fork-choice rule starts from the latest justified checkpoint” is because of the locking paradigm. In locking-based approach, a validator who have voted for a checkpoint whose parent (“source” in FFG) checkpoint is justified in the previous epoch is locked on the parent checkpoint; he cannot vote for any conflicting checkpoint until he sees a new later justified checkpoint. Therefore, there is always a possibility that some validators locked on a justified checkpoint unless you know another justified checkpoint later than that which unlocks the locked validators. If honest validators locked on a checkpoint, that checkpoint is the only one which we can assume that a sufficient number (2n/3) of honest validators can vote for (so “stuck-free”) only by the t < n/3 assumption. This is why we start the fork-choice rule from the latest justified (not finalized!) checkpoint.

In a leaderful approach, validators vote for the view decided by a leader. In full synchrony, the voting succeeds if the leader is correct because the correct leader can pick up a correct view such that no other validator is locked on a conflicting chain.

Our solution

From the view of locking paradigm, in a bouncing attack, the attacker is misleading honest validators as if some honest validators are locked on it. Our solution simply uses a synchrony assumption that the delay of votes are up to k slots and hence votes delayed more than k can be considered adversarial when the network is normal.
Even when honest votes are actually delayed by a temporal network failure and some validators are locked on a checkpoint which you find justified more than k slots later, the protocol is stuck-free because validators can catch up at the start of the next epoch.
Notably, this approach is still leaderless and simple.

Future works

• Liveness proof of fixed FFG (Make sure that this fix does not introduce a new problem)
• Incentive analysis

[vbuterin]

If you set k = \frac{1}{3} - \epsilon, then if fraction 2\epsilon of validators are offline and the attacker causes a fork right before k, then honest validators would not be able to cause justification, as they would only have (\frac{2}{3} + \epsilon) * (1 - 2\epsilon) \approx \frac{2}{3} - \frac{\epsilon}{3} validators slots, correct? So you would want to set k to equal something like \frac{1}{6}?

But then what is the total number of (offline honest + attackers) that FFG can survive with this modification?

Splitting attack

Can we try to mitigate this by borrowing techniques from 99% fault tolerant synchronous consensus? For example, have a mechanism where the maximum time at which you can switch over depends on the percentage of validators that you see switching over, so if you reach one validator on time then that validator would support the new chain and their added signature increases the time limit before which other validators would accept the new chain.

Also, what do you think of the “switch at most once every three epochs” technique proposed in Beacon chain Casper mini-spec ?

[nrryuya]

The fault tolerance for safety & liveness would be still 1/3.
When an attacker published a new justified checkpoint in a conflicting chain in the first k slots, honest validators might not be able to justify a new checkpoint in that epoch (and it is the same in the original FFG) but they can justify a checkpoint in the next block (under full synchrony).

Setting k small is better to prevent an attacker from doing this 1 epoch justification failure. Because in this case there are no honest validators locked on the new justified block, honest validators can ignore the checkpoint justified by the attacker and justify the original checkpoint.

The exact condition on k to prevent the 1 epoch justification failure is as follows.
Here, k' is a ratio k/\mathrm{SLOTS\_PER\_EPOCH} and x is the ratio of offline nodes.
For justification to happen,
(1 - k')(1 - x) \ge 2/3
\iff k' \le (3x - 1)/(x - 1)/3

(Ref: Google)

However, there is a trade-off of k. When a subset of the honest validators received a new checkpoint with delay \Delta (e.g. due to their local network failure) and the other validators have already voted for and are locked on it, they can switch and hopefully succeed in justification in this epoch if \Delta < k (depending on the slot allocation).

For example, have a mechanism where the maximum time at which you can switch over depends on the percentage of validators that you see switching over, so if you reach one validator on time then that validator would support the new chain and their added signature increases the time limit before which other validators would accept the new chain.

Yep! I think there would be more “smoother” kinds of approach by taking other validators’ opinion into account.
That’s being said, I tried to propose something easy to reason about and simple to implement potentially for Phase 0 or 1.

Also, what do you think of the “switch at most once every three epochs” technique proposed in Beacon chain Casper mini-spec?

In that approach, if there are two honest validator sets both of whose sizes are less than 2/3 accepted conflicting latest justified checkpoints due to temporal asynchrony, doesn’t it take at least three epochs for them to get on the same chain and start justification?

[vbuterin]

@nrryuya

if there are two honest validator sets both of whose sizes are less than 2/3 accepted conflicting latest justified checkpoints due to temporal asynchrony, doesn’t it take at least three epochs for them to get on the same chain and start justification?

Yes, but the implied assumption is that asynchrony on the order of an epoch is going to be an extremely rare event so taking the hit is fine.

[nrryuya]

I agree that the “two validator sets accepted conflicting latest justified checkpoints” situation is rare but it is the situation which makes the unlocking rule necessary.

The three epochs locking scheme (or more generally, >1 epoch locking without the k slots of unlocking period) would be better than my fix basically when an attacker has a justifiable checkpoint conflicting with honest validators’ chain and k is set too small compared to x as I explained.
Also, in that scheme, splitting becomes somewhat difficult to start but possible when there are two justifiable & conflicting checkpoints. It causes >=3 epochs of justification failure and can continue recursively under the same assumption on the attacker’s ability.

[nrryuya]

I found a more complicated bouncing condition, which I didn’t cover in the previous analysis. Here, an attacker can start a bouncing attack against the above fix if k > 0.

Setting k = 0 fixes this, although this condition would be even less likely to be met in practice.

[lucian]

Could you please explain more specifically in which case it will happen? Will it happen under FMD? Thanks!