Horn: Collecting signatures for faster finality
Authors: George Kadianakis <@asn>, Francesco D’Amato <@fradamt>
![]()
This post proposes Horn, a two-layer signature aggregation protocol which allows the Ethereum consensus layer to aggregate attestations from the entire validator set, every slot, even with 1 million validators. This is a significant increase compared to the status quo where the consensus layer is aggregating attestations from 1/32 of the validator set.
Motivation
Ethereum uses BLS signatures to aggregate consensus votes in every slot. Right now, 1/32-th of the validator set is attesting in every slot, so that every validator votes once per epoch. However, there are immense consensus protocol benefits to be reaped if every validator could vote in every slot:
- Faster finality: with one full voting round per slot, we could finalize in two slots. With two, in a single slot. By itself, this has multiple important consequences:
- Better confirmation UX: users (including exchanges, bridges) can quickly rely on economic finality.
- Reorg prevention, mitigating the possible destabilizing effects of MEV
- Provable liveness: it is much easier to guarantee that the consensus protocol will successfully finalize something if everyone is able to vote at once, because we only need to ensure short-term agreement on what needs to be finalized. For example, proposers can be used as a coordination point.
- Enabling LMD-GHOST, the current available chain protocol, to be reorg resilient and provably secure. Together with a better interaction mechanism for available chain and finality gadget, this is one of the two major steps towards an ideal consensus protocol for Ethereum.
This post focuses on signature aggregation. Please see Vitalik’s post on Single Slot Finality for more details on the consensus side of things, and further discussion of the benefits.
Proposal Overview
With Horn, we aim to keep most of the current signature aggregation logic intact, while adding another layer of aggregation on top of it. We still organize validators in committees of size 1/32-th of the validator set, but this time every such committee votes in every slot, instead of once per epoch. This way, we ask validators to do the same amount of burst work they are currently doing, but more frequently. We also add an additional layer of signature aggregation, which reduces the communication costs required to process attestations.
In the following sections, we delve deeper into Horn. We start with a small introduction to the current aggregation scheme. We then present a strawman intermediate proposal that motivates Horn. Finally we present the Horn protocol and discuss its security properties.
Introduction to the current aggregation scheme
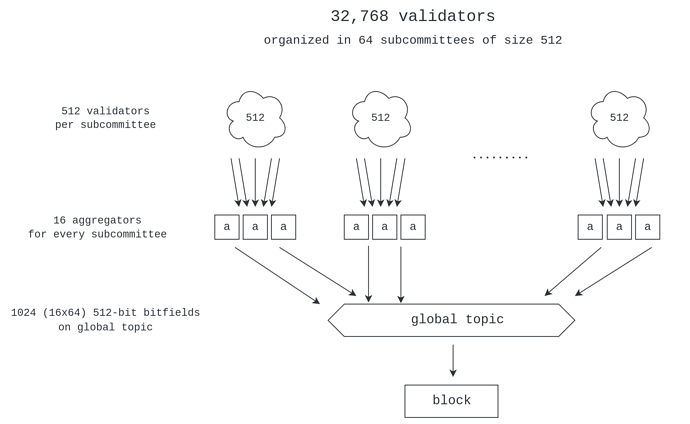
In this section we highlight some features of Ethereum’s current aggregation scheme that play an important role in the design of Horn. Here and in the rest of the document, we will always refer to a validator set size of 1M, or 2^{20}. A single committee is 1/32 of that, i.e. 2^{15} = 32768 validators.
For the rest of the document we assume that the reader is already familiar with Ethereum’s
current signature aggregation scheme which is depicted in the figure below.
Communication costs on the global topic
Blockchains use signature aggregation to amortize signature verification time and bandwidth:
The block proposer needs to include votes into the block. To do this, the block proposer monitors a global topic channel in which validators send their votes. Moreover, every full node must listen to the global topic as well, in order to follow the chain, because computing the fork-choice requires attestations from other validators.
If we didn’t do any aggregation, every validator would need to send their vote into the global topic, which would be overwhelming both in terms of bandwidth and in terms of verification time. By adding a layer of aggregation, we essentially reduce the work that all nodes have to do to see and verify those signatures.
For this reason, minimizing the global topic bandwidth is a central part of this proposal.
A strawman proposal
First, let’s try to naively extend our current one-layer aggregation scheme to 1M validators. This way we can shed additional light into the bandwidth issues that arise without further aggregation.
The simplest way to scale to 1M validators is to increase the number of subcommittees. Ethereum currently gets 32,768 validators to vote every slot using 64 subcommittees. This means that we can get 1M validators to vote every slot using 32*64 = 2048 subcommittees.
With 16 aggregators per subcommittee, we end up with 32768 aggregate bitfields of size 512-bits into the global topic. Now observe that the size of the two BLS signatures which accompany the bitfield, the aggregate signature and the signature of the aggregator, would be another 192 bytes (3x the size of the bitfield), and overall bitfields and signatures add up to 8MBs. Hence, the overhead of this naive proposal quickly becomes prohibitive.
To address this issue, in Horn we add another layer of aggregation to reduce the amount of messages on the global topic. We will see that Horn requires 512 aggregates with bitfields of size 32768-bits on the global topic, which dramatically lowers the communication cost there, in two ways. Firstly, the number of messages is reduced by a factor of 64x. Moreover, while the size of the bitfields increases by the same factor, the size of signatures does not, and becomes essentially negligible. Overall, we need 2.1MBs instead of 8MBs, almost a 4x improvement.
In the next section we dive into Horn.
Horn Protocol
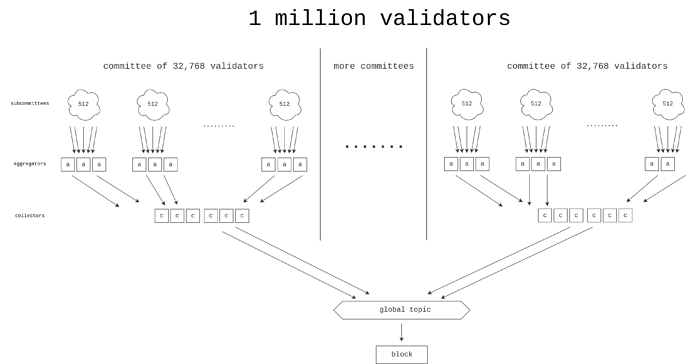
The basic idea of the Horn protocol is that we reuse the existing aggregation scheme within each committee, in parallel, and then add a new aggregation layer managed by a new network entity called collectors.
Collectors are tasked with collecting aggregates from each subcommittee (which contains 512 validators) and aggregating those further into collections which represent entire committees (which contain 32768 validators).
Collections are then sent to the global topic. With this additional layer of aggregation, we reduce the amount of messages that reach the global topic from the previous 32,768 to 512.
Collectors
We assign 16 collectors to each subcommittee, the same way we currently assign aggregators to each subcommittee.
Collectors are tasked with collecting aggregates across different subcommittees and aggregating them into collections. A collection consists of an aggregated BLS signature and a bitfield of size 2^{15}-bits.
Observe that collectors are asked to aggregate the bitfields they receive from subcommittee aggregators. The collector’s job is to produce the best possible collection representing the entire committee. To achieve that, the canonical strategy for collectors is to pick the best aggregate from each subcommittee and aggregate them further, which is possible since different subcommittees do not intersect.
If each committee of 2^{15} validators has 16 collectors, and we have 32 such committees, we end up with 512 collections on the global topic.
Slot time increase
This proposal requires an additional round of communication for the new aggregation layer. At the moment, we allocate 4 seconds to each round of communication, so this suggests that a slot time increase of at least 4 seconds might be necessary. In our case, more time is likely required, because of the high verification overhead involved.
In the status quo, the global topic sees 1024 aggregates with bitfields of size 512-bits, but with Horn the global topic sees 512 collections with bitfields of size 2^{15}-bits. Verifying an aggregate (or a collection) involves reconstructing the aggregated public key using the bitfield, and then verifying the signature. With Horn the bitfield grows significantly and this increases the verification time.
To give enough time for the verification of collections, we propose increasing the slot time by 10 seconds. We argue that the benefits of Single Slot Finality are so great, that the increase in slot time is excused. To back our proposal, we provide concrete numbers on verification time and communication costs in the next section.
Cost analysis
We will only discuss the costs in the global topic, because all costs borne by subcommittees and committees are already well understood, as they are incurred today on attestation subnets and the global topic.
Verification time for collections
Thanks to Mamy Ratsimbazafy for the help with optimizing and benchmarking verification
The global topic receives 512 collections. To optimize verification time, we observe that reconstructing the aggregated public key is a big sum of a maximum of 2^{15} BLS12-381 G1 points.
Such big sums can be amortized using bulk addition algorithms: these algorithms are based on the fact that inverting field elements is the expensive part of adding two elliptic curve points. The insight of these algorithms is that the field inversions can be amortized when adding many points at once by doing a single Montgomery batch inversion at the end. In our testing, this technique provides a 40% speed up over performing the summation naively.
Here are the results of our benchmarks for verifying 512 collections with bitfields of size 2^{15}-bits:
- 2.8 seconds on a
i9-11980HK(top laptop CPU from 2021) - 6.1 seconds on a
i7-8550U(five years old CPU) - 36 seconds on a Raspberry Pi
The above results can be improved significantly because:
- The verification operation is embarassingly parallel but our code is not threaded. For example, if we spread the 36 seconds work in rpi4’s four cores, it would take 9 seconds. On a normal consumer laptop like the second one, it would only take 1.5s.
- We can optimize the verification by precomputing the fully aggregated public key over each committee. For this, we assume that committees are known enough in advance (which is also a requirement in order for validators to have time to find peers in their attestation subnets), and that they do not change too often. We can then choose whether to reconstruct an aggregate public key directly or by subtraction from the full aggregate over its committee, based on whether the bitfield contains more ones or zeroes. If there’s more ones, we substract, i.e. pay the cost for subtracting up the public keys whose bit is set to zero, and if there’s more zeros we add, i.e. pay the cost for adding up the public keys whose bit is set to one. This way, we get a speedup of at least 2x over the naive approach.
- Under normal circumstances, the beacon chain participation rate is > 95\%. This means that the bitfields will have a really heavy Hamming weight. Reconstructing the aggregate public keys by substraction will then take a small fraction of the naive reconstruction time.
- The rpi4 benchmarks don’t include assembly code and we estimate that the operation would be about 20% faster with assembly.
- All relevant operations can be significantly optimized with GPU support
Bandwidth overhead
Aside from the verification time, we also need to make sure that we are not straining the network in terms of bandwidth.
In this new design, the global topic sees 2MB of bandwidth in these 10 seconds (512 collections with bitfields of size 2^{15}-bits). While this is a significant number, it’s also roughly equal to the EIP-4844 max blob data per block and the current max calldata per block. If 200KB/s of burst bandwidth ends up being too heavy, we might have to increase the collection time further than 10 seconds.
However, regardless of burst bandwidth, this proposal significantly increases the sustained bandwidth requirements for nodes. Right now nodes receive and transmit an average of 390KB/s when not subscribed to any subnets and 6-7MB/s when subscribed to all subnets, with bandwidth ramping up pretty linearly between those two points. Hence this proposal would substantially increase the bandwidth requirements for home stakers, which is already a sore point.
We note that the above numbers assume that bitfields are transferred naively. In the real world we would probably use Snappy compression. Such compression would significantly improve bandwidth usage under normal circumstances where bitfields have a very high Hamming weight. Under adversarial circumstances, nodes could avoid compressing based on an overhead threshold.
Beacon block size increase
Today, blocks contain a maximum of 128 attestations. At 1M validators, these have size 288 bytes (128 bytes for AttestationData, 96 for the signature and 64 for the 512-bit bitfield), so a total of about 37 KB per block. With Horn, we would have 64 attestations per block (keeping a 2x redundancy factor to account for missed slots etc…), each with a 32768-bit bitfield, so a total of about 276 KB. Part of the slot time increase can be allocated to increase the block propagation time to account for this. The remaining issue is storage, with a day of Beacon blocks amounting to over 2 GB. We argue that this is not really an issue, as normal validators have no reason to keep around the entire history of the chain, and it should still be possible to store blocks for weeks in case the chain is not finalizing.
Reward griefing attacks against Horn
While Horn is a straightforward aggregation protocol, it also contains a reward griefing attack vector.
Recall that Alice, a collector, receives multiple aggregates per subcommittee. She then chooses the best aggregate from each subcommittee, and adds it to her collection which represents an entire committee.
This “choose best aggregate” behavior opens the protocol to a reward griefing attack: Eve, a malicious aggregator (who also controls N validators) can always create the best aggregate by stealing the second best aggregate, removing N-1 honest public keys, and adding her own N public keys.
This way Eve always has the best aggregate, which allows her to grief other honest validators by removing their contribution from the bitfield, preventing them from being rewarded for their vote. It’s worth pointing out that this attack is also possible in the current system since the proposer can always choose which attestations get included in the final block, which is ultimately what determines the rewards.
In the appendix we touch on potential interactions about this attack and the consensus logic, and we argue that they are not harmful.
Alternative aggregation schemes
In this section we look at ways to fix the reward griefing attack vector.
When aggregators send an aggregate signature, they also send a bitfield indicating the identities of the validators who signed the message.
It’s important to note that two overlapping bitfields from the same subcommittee, for example (1,0,0) and (1,1,1), are not possible to get aggregated further with a bitfield: further aggregation would require specifying the multiplicity with which each signature appears in the aggregate signature, for example (2,1,1) in this case.
The reward griefing attack above stems precisely from the fact that Alice is unable to aggregate overlapping bitfields, and hence she must choose the best aggregate from each subcommittee. If Alice could aggregate overlapping bitfields, she could just aggregate all 16 bitfields into her collection, addressing any such attack, because she would always include some aggregate from a honest aggregator, which would in turn include all honest votes from their subcommittee.
Let’s look at some alternative aggregation schemes that allow us to aggregate overlapping bitfields.
| Reward griefing | Bandwidth | Verifier Time | |
|---|---|---|---|
| bitfield | |||
| uint4 | |||
| succinct proofs |
Aggregation with four-bit integer vectors
The naive fix to this issue is to allow the aggregation of overlapping bitfields. We can collect up to 15 (out of the expected 16) overlapping aggregates from the same subcommittee by using a vector of four-bit integers to encode the multiplicity.
The main issue with this approach is that this blows up the communication costs by a factor of four, since now we need four bits for each validator instead of a single bit. We now need to gossip 8MBs on the global topic.
Aggregation using SNARKs
Thanks to Nalin Bhardwaj, Mary Maller, Dan Boneh, Andrew He and Scott Wu for designing the custom proof system detailed in this section
It shouldn’t come as a surprise to most readers, that this problem can also be solved with… zero knowledge proofs. And by zero knowledge proofs we mean “succinct proofs” because we actually don’t care about zero knowledge in this case.
It’s well known that you can design SNARKs that prove that legitimate signatures were aggregated correctly. However, such proving systems are too slow (on the prover side) for our use case.
One way to work around this is to prove a simpler statement: That a provided public key is the result of aggregating certain public keys together with certain multiplicities.
It’s possible to design such a custom proof system using Bulletproofs-like IPAs. The resulting system has a logarithmic-size proof: about 3 kilobytes are needed to prove the aggregation of an aggregated public key consisting of 2^{15} public keys.
The main issue with this approach is that the naive Bulletproofs verifier is linear on the size of the witness. This effectively means that verifying such a proof takes about half a second, which renders it impractical since we need to verify 512 of them.
While IPAs can be batch verified in traditional blockchain settings, our case is slightly more complicated. That’s because adversaries can flood the P2P network with corrupted proofs that will cause the batch verification to fail. In that case, we would need to resort to group testing to find the offending proofs.
Finally, there are modifications to IPAs that allow us to move to a logarithmic verifier, but that would require us to use a commitment scheme on the G_t target group which makes computations significantly slower. Whether it’s worth doing so, is still pending research.
Future research
Wrapping up, we present some open questions that require further research:
- Are Horn’s bandwidth requirements acceptable? How can we get greater confidence here using simulations etc.
- Investigate how stateless/stateful compression techniques can reduce bandwidth usage on the global topic.
- We currently elect 16 aggregators to be almost certain that we will never end up without at least one honest aggregator. However, the number 16 acts as an amplification factor for the bandwidth in this proposal. Are there other election mechanisms we could use for collectors that would allow us to end up with less collectors?
- What other bitfield aggregation schemes exist? Can we improve the proof-based scheme?
- We can tune the size of committees to control the number and size of messages on the global topic. We can tune the size of subcommittees and committees to control the load on them and on the global topic (e.g. reducing the size of committees increases the load on the global topic but decreases the load on each committee). What are the right numbers?
- What are the minimal conditions for deploying a protocol like Horn, and switching to everyone voting at once? In particular, what changes are needed at the consensus protocol level, if any? The most relevant area of research is the interaction between FFG and LMD-GHOST, since the “surface area” of this interaction is very much increased by having everyone voting at once, because we now justify much more frequently. It seems likely that changes to the existing interaction mechanism (which are actively being explored) would be required in order to ensure that known problems are not aggravated.
Appendix
Censorship attack implications on consensus
The acute reader might notice that the above censorship attack could also impact the LMD-GHOST fork-choice. We briefly argue here that this is not the case.
Note that each censored vote can be uniquely mapped to an equal adversarial vote, since N adversarial votes are required to censor N honest votes. Therefore, we only need to show that any single substitution of a honest vote with an adversarial vote for the same block does not give the adversary additional control over what the outcome of the fork-choice is, in the sense that they could have always cast their vote in a way which would have produced the same result, without needing to censor the honest vote. Say that the latest message of the honest voter prior to the censored vote was for block A, and that their censored vote is for block B. The censorship attack results in the votes which count for the fork-choice being A by the honest voter, due to B being censored, and B by the adversary, since censoring requires them to also vote for B. If instead the adversary had not censored, the votes would be B and the latest message of the adversary, which can be any vote chosen of their choice. The adversary could then just vote for A, leading to the same outcome.