Batch Deposits for [op/zk] rollup / mixers / MACI

[barryWhiteHat]

Thanks to John Adler for review and feedback.
Thanks to Ying Tong for feedback and providing images.

Intro

In a bunch of different projects we need to allow the user to deposit from the EVM into some off-chain state which is represented on-chain as a Merkle accumulator (e.g. the root of a Merkle tree). This Merkle tree is updated by validity proof (e.g. a SNARK) or a fraud proof + synchrony assumption.

SNARK-friendly hash functions are very expensive, so minimizing this cost is useful. In optimistic rollup world it is not as expensive, but having a cost for each deposit limits certain usecases, such as mass migrations.

To deposit from the EVM into a Merkle tree you need to perform tree_depth hashes in order to include a leaf. Even if there are two deposits in a block they both cost tree_depth hashes. It would be nice to merge these together so that they only cost tree_depth + 1 hashes.

These deposits are O(n * \mathtt{tree\_depth}). Here we propose a method of deposit batching that is O(n + \mathtt{tree\_depth}). In a companion post we apply these optimizations to mixers and optimistic rollups.

Previous Work

Merkle Mountain Ranges are focused on creating Merkle trees whose depth grows over time. In this usecase we need to have a constant-depth tree as is fixed and cannot have variable number of hashes. In optimistic rollup this is not ideal either because as your tree depth grows the data that you are required to put on-chain changes.

Using this for deposits is problematic because peak bagging becomes rarer as the set gets bigger so deposits can become very rare. Which could lead to users waiting indefinitely for their funds to be deposited.

Another approach is multiproofs. This cannot be used here because it requires coordinator between depositors. Given a deposit que that is constantly changing it is likely that the state will have changed before the coordinated update gets processed.

Method

Deposit Queue Creation

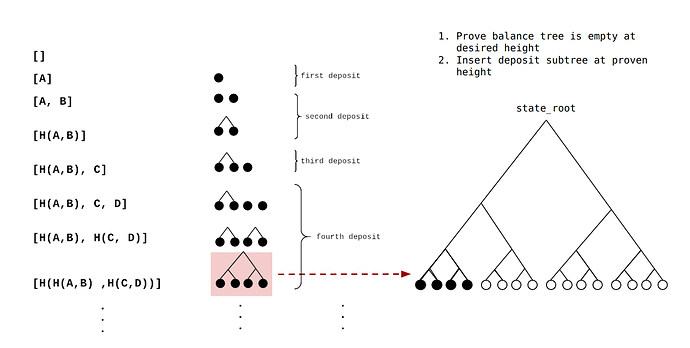
If you ever played the 2048 you may have derived pleasure from merging two blocks of the same value together. We do this here but for Merkle trees.

We start with an empty deposit tree. When a deposit comes in we store that in the queue and wait. When the next deposit comes in the hash this and save this hash as our current deposit_tree with depth 1 with 2 pending deposits. We then can stop storing any data related to the first deposit.

When another deposit comes in we store it again. Then for the next deposit we hash it with the qued value and then hash the result with the deposit tree. To create our deposit tree with depth 2 with 4 pending deposits.

We have effectively merged deposits together.

Insert deposit_tree into balance_tree

So at this point we have a deposit tree which is depth 2 with 4 pending deposits. We also have a balance_tree which contains some accounts that have previously been deposited and zeros everywhere else. We don’t want to overwrite the accounts in the tree. Because this would destroy these users accounts. We only want to replace zeros.

In order to insert the new leaves into the balance tree we need to prove that:

1. That a node has all zeros children. We need to do this to prevent overwriting already-deposited accounts.

Lets take an example say that we have a node at with 2 children. We know that if the 2 children are 0 then the node == hash(0,0).

But if the tree is really deep it might not be efficient to compute this hash in the EVM/SNARK. So instead pre-compute this list and deploy the smart contract with this stored as a mapping.

Tables	Are
Layer 1	hash(0,0)
Layer 2	hash(hash(0,0), hash(0,0))
…	…
Layer Tree_Depth	hash(hash(hash(…hash(0,0),))…)

Then whenever we want to check that a node has all zeros children we just look up this mapping.

So someone proves that the node is in the tree with a Merkle proof and then proves that it has all zero children by checking the stored mapping.

2. The new Merkle root has only the zero node changed with everything else the same.

We have previously proven a leaf has all zero children and now we want to change that leaf while keeping the rest of the tree the same.

Using the same Merkle path we calculate the root with the zero leaf replaced with the deposit_tree.

We then store this new Merkle root as the new balance tree which contains all the deposited leaves. Using the same Merkle path that we used to prove that the leaf was in the tree holds all other leaves constant and only allow us to update the children of the zero node.

Note on syncronousity

Some systems like zksnarks/optimistic rollup require proving time before the deposit can be executed. If the deposit_tree changes while this is happening the proof could be invalidated. So it would be good to have a method to pause updates to a certain deposit tree while it is being deposited.

Summary

Here we have proposed a method of merging deposits. We que deposits in the EVM and them merge them when they are deposited into the bigger merkle tree.

In a follow up post we will apply this to mixer deposits and optimistic rollup deposits / mass migrations.

[weijiekoh]

Let’s say the queue length is 8 instead of 4.

Let storage be the amount of gas needed to store one value.
Let hash be the amount of gas needed to hash two values.

Deposit #	storage	hash
1	1	0
2	1	1
3	1	0
4	1	2
5	1	0
6	1	1
7	1	0
8	1	3

This means that users 2 ^ n are at a disadvantage just by virtue of their position in the queue.

[barryWhiteHat]

Its still cheaper for everyone when compared to the status quo tho ?

[weijiekoh]

It is indeed cheaper for everyone

IMO, the severity of this tradeoff is a matter of preference, while taking into account the cost per hash.

If the hash function is cheap (e.g. Keccack), then the cost difference is negligible, but the gas costs for the 2^n-numbered-users add up if the hash function is expensive (e.g. Poseidon)

[vbuterin]

Kate commitments are worth exploring for this purpose. With Kate commitments it’s easy to prove an arbitrary number of positions from a single state with just one group element (48-96 bytes). This could be combined with the queue approach to make sure that there’s a lot of deposits that can be batched together. The other benefit of the Kate approach is that it’s easy to plug it into an elliptic curve based SNARK/PLONK proof.

[weijiekoh]

What do you have in mind with using Kate commitments? Is the idea to accumulate all the deposit subroots into a Kate commitment instead of a balance tree?

[vbuterin]

The deposits and the balances.

[weijiekoh]

I see! Though to verify a Kate commitment in a snark is still not feasible with the best dev tooling we have (BN254 with circom). Feel free to push back but IMO, we have to wait till more advanced snarks are accessible for this technique to be practical.

[vbuterin]

Oh I’m not thinking of having a snark literally verify an elliptic curve pairing computation. I’m thinking of having a PLONK-like polynomial proof, where the Kate commitment and the opening are passed in as two of the arguments and you just do polynomial checks directly over those. So there’s no “one system verifying another system” overhead.

[weijiekoh]

Thank you! To clarify, is this the snark you have in mind?

public input kateCommitment
private input polyCoefficients[n]
public input openings[m]
public input indices[m]

srs = [...]

assert(kateComitment == commit(polyCoefficients, srs))

for i in range(0, m):
    assert(openings[i] == polyEval(polyCoefficients, index[i]))

In that case, it sounds like the commit() function (in the snark) would need an SRS and would also need to perform EC exponentiations to compute the Kate commitment. I might be wrong, but since it’s expensive to perform EC operations on existing SRSes which were done on alt_bn128, would we need to do a new a powers of tau ceremony over the BabyJub curve so that we can have snark-friendly Kate commitments?

[MichaelConnor]

Isn’t there a practical upper bound to the number of items which can be batched into a Kate commitment; the limit being the size of the SRS? If so, don’t Merkle Trees offer a much bigger anonymity set?

[vbuterin]

Thank you! To clarify, is this the snark you have in mind?

No no no I mean just directly doing a multi-proof on the Kate commitment. So you would have a commitment P that holds the state and you would just do a standard multi-opening that proves that P(x_i) = y_i for a set of (x, y) pairs.

You can go further: to avoid one EC multiplication per pair, the (x, y) pairs can themselves be encoded in polynomial commitments, and the multi-opening would turn into an equivalence proof: P(X(i)) = Y(i) (you can use standard PLONK tricks to prove this is true across a range), and then those polynomial commitments would simultaneously be part of a PLONK proof.

[weijiekoh]

[discussion reduce mode]

Maybe I’m looking at things from a different angle. I’m mainly concerned about gas costs for users, and secondarily, for the coordinator. This is after all what the batch deposit technique is meant to address.

In MACI, we need to prove things about each leaf in the balance tree in ZK. i.e in the balance tree (aka the message tree in MACI nomenclature), each leaf may or may not modify the state tree depending on its decrypted contents (e.g. a message leaf is an encrypted command which may change a user’s public key). Since we want to ensure that the coordinator processes each message in the correct order, our Groth16 snark has to prove each leaf’s membership and position in the message tree.

This already costs several hundred thousand gas. If we perform a Kate multi-proof that’ll add at least another 193k gas (the bulk of which is for the pairing check precompile).

If/when we move to PLONK (contingent on dev tooling), could we avoid this extra cost?

[discussion expand mode]

In the short term, without PLONK, perhaps there are benefits to using a Kate commitment in BabyJub so we can verify a Kate commitment or a Kate verkle tree inside our Groth16 snark.

1. Each user who deposits into a deposit queue only pays to store 32 bytes.
2. Once the deposit queue is full, the coordinator accumulates then into a Kate commitment, which should be cheap. To Kate-commit to 16 values, for instance, costs 223454 gas, which is a great improvement over a Poseidon binary Merkle tree, which needs 797835 gas to commit 16 values. This way, both users and coordinators save gas.
3. To construct the final balance tree, the coordinator would also use Kate commitments, resulting in a Verkle tree. Since we can commit to more values at a lower gas cost, we can have a much larger tree capacity.
4. When we process the balance tree (aka the message tree), we check the membership and position of each message inside the snark, and proceed as usual.

[weijiekoh]

Perhaps we could use Verkle trees (Merkle trees that use Kate commitments as the hash function instead of Poseidon/MiMC).

[Pratyush]

KZG10 commitments require pairings; BabyJubJub is not a pairing-friendly curve

[weijiekoh]

Ahh, totally missed this. Thank you!

[weijiekoh]

It’s possible to save even more gas with this technique. The hash function for the subtrees can be SHA256, which is cheap in the EVM. The rest of the tree (from the subtree depth to the root) can be hashed with Poseidon.

The tradeoff is that any snark circuits will increase in size by around 90k constraints per subtree level. To put this into perspective, Tornado Cash’s withdraw circuit has 28271 constraints. As such, this approach only makes sense for use cases like MACI where the prover may not mind (roughly) doubling or even tripling their proving time.

[JangoCCC]

It seems that if the same address makes two deposit operations, it will result in two nodes on the Merkle tree, how to solve this problem?