LMD GHOST with ~256 validators and a fast-following finality gadget

[vbuterin]

Epistemic status: early exploration

Recently, there has been discussion about more aggressive ways to reduce Ethereum’s slot time. This can be done in two ways:

1. Reducing the \delta parameter (our assumption on maximum expected network latency). This can only be done safely if we get improvements at the p2p layer that reduce latency
2. Re-architecting the slot structure to reduce the number of network latency rounds in one slot.

There is significant p2p hardening and optimization work going on to enable (1); the top candidate for enabling a significant speedup is erasure coding. Research work is focusing on (2).

This post will argue that the optimal approach to (2) may be to move somewhat away from the tight coupling between slots and finality introduced in 3SF, and instead have a more separate LMD GHOST fork choice rule and finality gadget, with different participant counts.

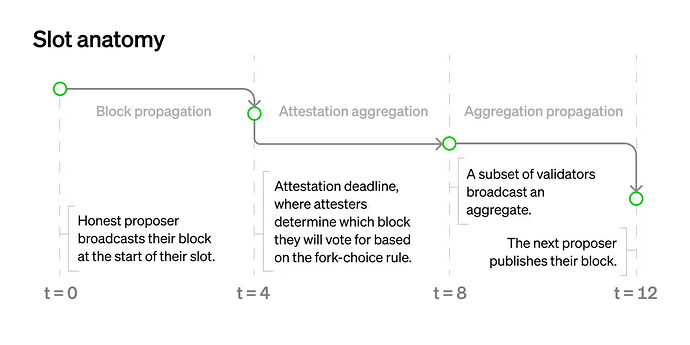
First, let’s look at the current slot structure (source):

\delta here is 4 seconds. The first section (block propagation) is unavoidable. Now, notice that there are two stages related to attestations: aggregation and propagation. This takes place because there are too many attestations (~30,000 per slot) to gossip directly. Instead, we first broadcast a subset inside of a subnet, and then we broadcast aggregates inside of a global p2p network.

If we were to increase the validator count much more (eg. to 1 million per slot), we may have to go up to three stages to keep the size of each stage manageable (indeed, previous writing suggested exactly this).

In general, we can approximate:

aggregation\_time = log_C(validator\_count)

Where C is the capacity: how many signatures can be safely simultaneously broadcasted within a single subnet. It seems like realistic values for C are in the hundreds or low thousands. If we want to be quantum-resistant, we should assume more conservative numbers (eg. if a quantum-resistant signature takes up 3 KB and there’s 256 of them per slot, that’s 768 kB per slot, roughly similar to worst-case execution block sizes).

Finality depends on the “full validator set” participating; perhaps 8192 if we either (i) accept more staking centralization or mandatory delegation or (ii) do Orbit, and much more (likely 10^5 to 10^6) otherwise. That is, either C^2 or C^3 depending on our assumptions.

Meanwhile, a stable LMD GHOST instance only requires a randomly selected quorum participating; here, size 256 (ie. less than C) is acceptable to achieve very low failure rates.

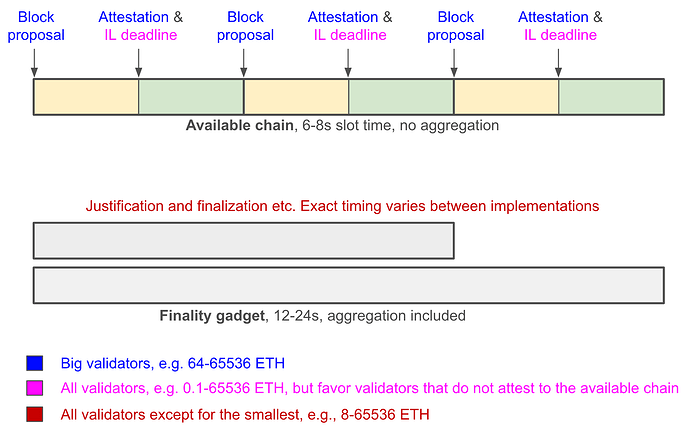
What this implies is that any approach that attempts to do one step of finalizing consensus per slot will inherently take 3\delta or 4\delta (adding in one \delta for the proposer). Meanwhile, if we don’t do that, one step will only take 2\delta.

This brings me to my key proposal:

1. Have an LMD GHOST chain where ~256 validators are randomly selected per slot. Use this as the primary “heartbeat”
2. Have a finalizing consensus mechanism trail closely behind (realistically, finalize in perhaps 12\delta), that uses all the active validators. Don’t try to couple LMD GHOST votes and finalizing consensus votes; treat them as fully separate.

This gives us the following benefits:

1. Very fast slot times that are good enough for the normal case, without changing any security assumptions (because the “aggregation” step is no longer part of the slot time)
2. We get much more freedom to choose a finalizing consensus mechanism, including taking off-the-shelf traditional ones (eg. Tendermint), although we do need to think about compatibility; roughly, “prepared” chains need to win the fork choice rule (similar criterion to 2017-era PoW-based Casper FFG)
3. We get a natural answer for “how to handle inactivity leaks”: during an inactivity leak, the LMD GHOST chain continues, the finalizing consensus stops. The LMD GHOST chain itself then deteremines the progression of the inactivity leak, which determines when finalization can recover.
4. We get much more freedom to take more ambitious choices for the consensus step (eg. 1 ETH validator req and 1 million validators)
5. More simplicity, because there are fewer interaction effects, and because we can get higher valdiator counts without needing Orbit-like techniques.

[kladkogex]

A fantastic paper from two years ago shows that essentially all Byzantine problems (including blockchains) have O(N²) complexity in the number of nodes:

https://arxiv.org/pdf/2311.08060

This is a bit of an elephant in the room for me. I don’t fully understand how this result can be reconciled with the fact that many blockchains, including ETH, claim better than O(N²) finalization, where N is the number of nodes.

If you have one million nodes, N² = 1 trillion messages.

Do you Vitalik, understand how to reconcile the theorem above with the fact that Ethereum claims to be O(N) ? I mean no offence here, just generally curious.

[mart1i1n]

Great idea! But seperateing the GHOST vote and Casper vote may cause additional liveness failure as the best head of Casper may conflict with the best LMD GHOST head. It requries strict considertation.

[cwgoes]

Awesome to see faster finality getting attention in the Ethereum discourse!

@vbuterin

What this implies is that any approach that attempts to do one step of finalizing consensus per slot will inherently take 3C or 4C (adding in one C for the proposer). Meanwhile, if we don’t do that, one step will only take 2C.

Do you mean δ here? Somehow C seems to have changed from a measure of capacity to a measure of time, and I didn’t quite follow. Or do you mean the time it takes to broadcast/aggregate within a subnet?

@vbuterin

1. Have an LMD GHOST chain where ~256 validators are randomly selected per slot. Use this as the primary “heartbeat”
2. Have a finalizing consensus mechanism trail closely behind (realistically, finalize in perhaps 12C), that uses all the active validators. Don’t try to couple LMD GHOST votes and finalizing consensus votes; treat them as fully separate.

This combination reminds me a lot of Zcash’s ongoing “Trailing Finality Layer” research effort (docs here), which is a similar combination of a fast “heartbeat” block production without a full quorum and a slower “trailing finalization” mechanism which requires a full quorum, where the former can proceed ahead of the latter. In the case of TFL, the fast block production mechanism is PoW, not PoS, but this doesn’t actually seem to change the overall construction too much.

However, there is one clear design difference: Zcash’s TFL design picks bounded availability over liveness (in the case when the finalization mechanism is not working – similar to Ethereum’s inactivity leak), and I think they have pretty strong arguments for doing so. Quoting directly from the TFL book (direct link to this section):

Both the available protocol, and the subprotocol that provides finality, will be used in practice — otherwise, one or both of them might as well not exist. There is always a risk that blocks may be rolled back to the finalization point, by definition.

Suppose, then, that there is a long finalization stall. The final and available protocols are not separate: there is no duplication of tokens between protocols, but the rules about how to determine best-effort balance and guaranteed balance depend on both protocols, how they are composed, and how the history after the finalization point is interpreted.

As the finalization gap increases, the negative consequences of rolling back user transactions that spend funds increase. (Coinbase transactions do not spend funds; they are a special case that we will discuss later.)

There are several possible —not mutually exclusive— outcomes:

• Users of the currency start to consider the available protocol increasingly unreliable.
• Users start to consider a rollback to be untenable, and lobby to prevent it or cry foul if it occurs.
• Users start to consider finalization increasingly irrelevant. Services that depend on finality become unavailable.
• There is no free lunch that would allow us to avoid availability problems for services that also depend on finality.
• Service providers adopt temporary workarounds that may not have had adequate security analysis.

Any of these might precipitate a crisis of confidence, and there are reasons to think this effect might be worse than if the chain had switched to a “Stalled Mode” designed to prevent loss of user funds.

I think these arguments apply equally well to Ethereum, if not even more so, because Ethereum has a complex network of services (rollups, commerce, bridges, etc.) built “on top” which would need to decide what to do in such a scenario (where the finalization mechanism stalled for a long time). It may be helpful for the world to have at least one blockchain which prioritizes availability – but there are already many of those – and it’s not clear to me that it’s the best choice for Ethereum. Bounding availability in the case when the finalization mechanism is offline for an extended period creates a Schelling point for social coordination which would not otherwise be present. Is availability in the case of network partition really worth giving that up? Such an availability is dangerous, in my view, as it gives users the possibly mistaken impression that the network would be able to come to consensus in the future (which will not be known until the finalization mechanism is running again). Why not let layer 2s or other constructions built on top of Ethereum (maybe “local rollups”) maintain availability in such a scenario, while Ethereum itself prioritizes safety?

---

Minor note in response to the second post:

@kladkogex

This is a bit of an elephant in the room for me. I don’t fully understand how this result can be reconciled with the fact that many blockchains, including ETH, claim better than O(N²) finalization, where N is the number of nodes.

As far as I can see from a quick skim, this paper doesn’t take into account the possibility of message aggregation. In some sense, conceptually, there might still be 1 trillion messages, but you don’t need 1 trillion “actual” messages on the network if you can aggregate some of them (which is precisely what Ethereum does).

[vbuterin]

@kladkogex

Do you Vitalik, understand how to reconcile the theorem above with the fact that Ethereum claims to be O(N) ? I mean no offence here, just generally curious.

I think the papers count one-to-one pings whereas I count broadcasts?

[vbuterin]

Do you mean δ here? Somehow C seems to have changed from a measure of capacity to a measure of time, and I didn’t quite follow.

My bad, fixed.

Regarding availability, I’m very strongly pro liveness for these reasons:

1. In an extreme scenario where >1/3 of nodes go offline for an extended duration, chances are there’s something wrong with the social layer too, and so it’s ideal for the chain to be able to go through an inactivity leak and then kick back into full finalization mode all on its own.
2. If there is a 51% censorship attack, then it needs to be maximally easy for a minority to counterattack and make a minority soft fork, without having to coordinate too much. Being able to start an alternate chain with only a few people and then gather more and more momentum over time is much socially easier than having to hard fork.
3. If the chain splits because of a client bug, then historically it becomes clear which chain is correct long before all clients are updated and most or all nodes are once again following that chain. In such a split, allowing both chains to keep running allows people to individually immediately switch to the correct chain much faster than the whole network can do so, allowing many services to resume very quickly.

Most fundamentally, I start from the principle that it’s better to give people as much information about the future state of the chain as possible. This is the reason why shorter finality times are good, why finality is better than only having probabilistic fork choice, etc. From that same principle, if finality guarantees stop, it’s better to give people some information about the future state of the chain (via an available chain) than no information at all (via stalling).

In an ideal system, if the chain splits because of a bug, then it would even be able to finalize the idea of “either A or B” first, and then finalize one of the two later. This would give people whose transactions were included in both chains a strong assurance that their transaction would not be reverted. For sequencer-driven L2s, if the sequencer submits to both, then this effectively means that the L2 finalizes (with full security) even while the underlying L1 is going through a chain split. In fact, simple LMD GHOST already gives people synchronous confirmation of “A or B” in such a case: if A and B are both getting a large share of votes, it’s basically impossible for some other chain C to come in and become the head, unless suddenly almost all validators decide to change their view.

Also, more philosophically, I think we should be clear that Ethereum is striving to be “bitcoin-like”, and NOT “high-throughput-fast-chain-like”. The latter type of chain, of which there are many, will likely gravitate toward standard BFT with heavy implicit reliance on social consensus, because if you’re not prioritizing decentralization that approach is optimal. But if we are prioritizing decentralization, then we can’t count on a clean social layer that can easily make rapid decisions that everyone will agree on (as if such a gadget existed, it itself would be an unacceptable centralization risk), and so we need the chain to be able to proceed in ways that are social-layer-minimized even in extreme cases. Zcash has already taken the tradeoff of being more reliant on a powerful social consensus layer (eg. to determine recipients of the 20% dev issuance share), so it’s a very different system in that regard.

[potuz]

Apologies for using this as a braindump to come back later for notes. Say for the sake of concreteness that we can safely broadcast 512 signatures in about a second to the global network (we are looking at these numbers currently in the context of 7732). And we can broadcast and aggregate 35K attestations in about 6 seconds (which are the current numbers we are seing on mainnet). In this setting suppose we go to 4 seconds slots and we maintain 1.1M validators. With the naive approach of keeping broadcast for finality everything equal, this means that we need 1.5 slots to broadcast 35K attestations and therefore 48 slots per epoch. Every 3 slots we broadcast 70K attestations for the finalized checkpoint and in 16 such rounds we cover the entire validator set. This gives 192 seconds per Epoch instead of the current 384 but the gain does not come from the pipelining, but rather the full usage of the time for attestation propagation (from 12 seconds to 6 seconds).

If my understanding of the naive approach is correct then I believe a few things make the situation more effective. The finality votes being separated from head are much more aggregatable. Currently the only reason why we see different attestations is because of differences in the LMD vote. By removing this, we expect all (most) attestations to be the same except perhaps at slot 0. This should allow us to have less aggregates and therefore less aggregation propagation time, conversely we could probably pack many more attestations per 3 slots group rather than the 70K.

At any rate at this stage I see this proposal as a proposal to enable much faster blocks without compromising on security, perhaps with a little less reorg safety for proposers/builders. But not as a faster finality gadget except the first order approximation of enabling shorter slots.

[vbuterin]

this means that we need 1.5 slots to broadcast 35K attestations and therefore 48 slots per epoch

I’m not understanding this, where does 48 slots per epoch come from? I’m assuming a model where you do eg. 256 signatures per slot for LMD, and then separately you do 10k-1m signatures per ~3-6 slots. The load of the latter part is much higher, but it’s lessened due to aggregation, the only cost that cannot be cut through aggregation is the bitfield (1 bit per validator must be broadcasted globally).

Or are you trying to describe an approach that’s a much smaller delta from the status quo?

[potuz]

The 48 slots came from the assumption that 6 seconds is the required time to broadcast and aggregate 35K attestations (that was the number Xatu nodes were giving a few weeks back, but it seems newer data points to better numbers). Under that assumption, we need 3 slots for 70K attestations (each slot is 4 seconds) and thus in 48 slots we can handle 1,1120,000 attestations which is the whole validator set, thus we need 48 slots per epoch, each slot 4 seconds long which makes the epoch take half the time of today.

That is with the naive approach of keeping the whole attestation broadcasting for finality exactly as today. But given that aggregation will be perfect (except perhaps in slot 0) the numbers could be much better.

[rolfyone]

Increasing the number of slots is just kind of robbing Peter to pay Paul…

Why would we increase slot count rather than just selecting a slot duration that means we can maintain the same slot count we have now?

Eg. 48 slots at 4 seconds vs 32 slots at 6 seconds…

I guess the upside of less slots is less messages, but the down side is slower confirmation of a block…

[potuz]

Finality and latency are independent. I think the whole point of Vitalik’s idea as far as I can see is that we can have much better latency and shorter slots by decoupling LMD from finalization. Slot duration is decided by how fast we can propagate 256-512 votes (+ block execution/propagation) and and time to finality is decided by how fast we can propagate 1.1M votes (or whatever the total validator set is). The quotient between these two determines the number of slots per epoch you need and you have minimized both: slot time and finality time.

[saltiniroberto]

@potuz

The 48 slots came from the assumption that 6 seconds is the required time to broadcast and aggregate 35K attestations

Are you aware of any estimate of the relationship between the number of attestations to aggregate and the time taken?

Asking this as, if the relationship is sub-linear, then we can do better than 192s by trying to aggregate more than 35K attestations at the same time.

[potuz]

Yes, I agree as stated above that most probably the numbers I’m stating are just the most naive upper bound. I believe since aggregation will be perfect by decoupling LMD and getting all attestations equal, we may be able to aggregate many more attestations per slot.

[Nero_eth]

In the latest data I saw we were at 2s for 90% of attestations. And this is for missed slots.
For non-missed slots, where the load distributes better, we may see even lower number.
So, 70k attestations should be doable in ~4s, naively extrapolated.

[potuz]

This is only single attestations without the aggregation and rebroadcasting phase.

[fradamt]

If the goal was to aggregate 1M signatures as quickly as possible, without the added constraint of embedding this process into the critical path of the chain, I don’t think we would do aggregation just by doing the same thing we do today but with different parameters. For example, we could do two-layer aggregation like here, probably other things as well.

[aelowsson]

@vbuterin

This brings me to my key proposal:

1. Have an LMD GHOST chain where ~256 validators are randomly selected per slot. Use this as the primary “heartbeat”
2. Have a finalizing consensus mechanism trail closely behind (realistically, finalize in perhaps 12\delta), that uses all the active validators. Don’t try to couple LMD GHOST votes and finalizing consensus votes; treat them as fully separate.

Nice work. This reminds me very much of Consentrifuge (name cred shared with Barnabé ), which I proposed during one of the “Future of Staking” sessions in January. The difference is that I suggested that we can use an Orbit mechanism for selecting attesters to the available chain, in order to increase its stake weight. Note that the proposed timings are slightly outdated given our updated ambitions over the past months, but the approach remains the same.

The figure below illustrates the ceiling on the amount of stake we can recruit under a pure Zipfian distribution, depending on MaxEB. It is clear that the stake distribution for nodes is more favorable than a pure Zipfian distribution, and thus would allow for an even higher stake weight among attesters to the available chain. I account for this in current models, but not in this old figure.

I understand that a random selection of validators gives other favorable properties. It is not clear to me whether they outweigh the benefits of a heavier slowly rotating set.

[vbuterin]

@fradamt

If the goal was to aggregate 1M signatures as quickly as possible, without the added constraint of embedding this process into the critical path of the chain, I don’t think we would do aggregation just by doing the same thing we do today but with different parameters. For example, we could do two-layer aggregation like here, probably other things as well.

I was assuming a future based on STARK aggregation, where there isn’t that much difference between 2-layer, 3-layer, etc.

I think that up until the bound where broadcasting the bitfields starts to become a bottleneck, aggregation time will be more like log(nodes) than sqrt(nodes)

@potuz is right that if you fix to two-level aggregation regardless of node count, it becomes sqrt(nodes)

[kladkogex]

Well, I think the problem with aggregation is that a malicious aggregator may just refrain from doing its job. it is not as simple as it seems.

[kladkogex]

Well, then it is 0(N) of the number of broadcasts, hard to argue here

In reality what it means is each node needs to communicate once with every other node.

As far as consensus is concerned, I would love if ETH foundation had a competition, our consensus for example is way faster than Tendermint and is provably secure.