TL;DR
We present a simple fix on FFG which makes it difficult for an attacker to continue bouncing attack unless the attacker has strong control over the network.
Prerequisites:
(Definitions and notations borrowed from it)
Fix on FFG
In Casper FFG, the fork-choice rule does not start from the genesis block, but the latest justified checkpoint. (In this post we call the block from which the fork-choice rule starts start point.) Whenever a validator sees a new latest justified checkpoint, the start point changes.
We modify this so that the start point switches to a different chain only in the first k slots of every epoch. Specifically,
- When a validator see a new latest justified checkpoint and it is conflicting to the current start point,
- if his local clock is in the first k slots, he replaces his start point with it
- if it is not in the first k slots, he marks it as pending
- When a validator enters a new epoch, he recalculates the latest justified checkpoint for the start point from justified checkpoints he has ever seen including ones marked as pending
Here we require k is less than \mathrm{SLOTS\_PER\_EPOCH}/3 slots.
(See below for the reason.)
Security analysis
Here we describe how the above fix prevents a bouncing attack.
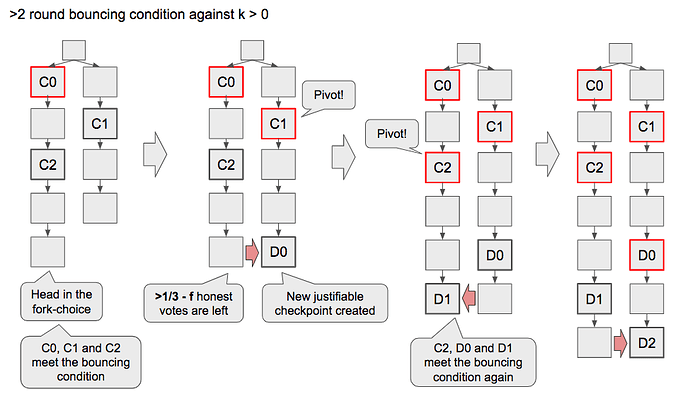
Assume at a certain time, the network becomes fully synchronous (the delay < 1 slot) and the bouncing condition is satisfied (i.e. honest validators’ start point is a checkpoint C and there is a later justifiable checkpoint C' conflicting with C ).
Let C'' be the checkpoint which the honest validators vote for in the beginning.
We argue that an attacker cannot make C'' justifiable.
In a case where there is no new latest justified checkpoint appears in the first k slots, honest validators succeed to justify C'' in this epoch.
In a case where an attacker justifies C' and publishes the votes in the first k slots, honest validators accept it as their start point. However, C'' cannot be justifiable because k < \mathrm{SLOTS\_PER\_EPOCH}/3 and hence \mathrm{FFGVotes}(C'') < n/3.
Therefore, the attacker cannot create a justifiable (but not justified) and conflicting checkpoint continuously so eventually bouncing stops when the attacker spends up all the justifiable checkpoints which are prepared before the network becomes fully synchronous.
Splitting attack
In the above argument, it is assumed that honest validators agree on whether to change their start point.
However, it is not always true because an attacker who has a strong control over the network can split honest validators; the attacker can send votes which justify C' to only a subset of the honest validators at the moment slightly before the end of k -th slot so that the recipients cannot gossip the information to other honest validators in time. By splitting, the attacker can make C'' justifiable by leaving an appropriate number of honest validators to C'' and making other validators switch to C'.
The exact condition for the attacker to make C'' justifiable is as follows.
- Let v_{C''}^H be the number of honest votes for C'' at the end of the k -th slot.
- Let x be the number of honest validators who is allocated to a slot after the first k slots and does not see C' justified in the first k slots.
- For C'' to be justifiable, x + v_{C''}^H + t \ge 2n/3 \land x + v_{C''}^H < 2n/3
- \therefore 2n/3 - v_{C''}^H - t \le x < 2n/3 - v_{C''}^H
This is one of the “last-minute delivery” family of strategies. This strategy requires the attacker to identify at least tens of thousands of (physical) nodes with validators (public keys) and to have almost direct connections to them. It would be much more difficult than the original bouncing attack.
Therefore, our fix on FFG prevents bouncing attack under the assumption that the attacker does not always succeed in last-minute delivery. Also note that if an attacker can do last-minute delivery, he can attack on the fork-choice by splitting the votes into and keeping the balance of two chains.
Rationale
In this section, we discuss the rationale of this fix from the perspective of BFT consensus theory.
Casper FFG as locking-based pipelined-BFT
Casper FFG is one of the pipelined-BFT protocols, where the consensus consists of two phases of voting and every vote is both for the first phase (“pre-commit”) of the target checkpoint and the second phase (“commit”) of the direct parent checkpoint.
(Related works are Hotstuff and Pala.)
Also, Casper FFG adopts locking paradigm a la Tendermint in the form of slashing conditions, instead of view-change voting a la PBFT.
The difference between FFG and the other existing works is that FFG is leaderless; chain-based pre-consensus is used to create checkpoints and there is no fixed view (i.e. the checkpoint which validators can vote for) chosen by the leader of every epoch.
The advantages of this approach are (i) no security/performance loss due to leader’s failure and (ii) flexibility of the tradeoff between time to finality and number of validators.
Why “fork-choice starts from the latest justified checkpoint”?
The rule that “the fork-choice rule starts from the latest justified checkpoint” is because of the locking paradigm. In locking-based approach, a validator who have voted for a checkpoint whose parent (“source” in FFG) checkpoint is justified in the previous epoch is locked on the parent checkpoint; he cannot vote for any conflicting checkpoint until he sees a new later justified checkpoint. Therefore, there is always a possibility that some validators locked on a justified checkpoint unless you know another justified checkpoint later than that which unlocks the locked validators. If honest validators locked on a checkpoint, that checkpoint is the only one which we can assume that a sufficient number (2n/3) of honest validators can vote for (so “stuck-free”) only by the t < n/3 assumption. This is why we start the fork-choice rule from the latest justified (not finalized!) checkpoint.
In a leaderful approach, validators vote for the view decided by a leader. In full synchrony, the voting succeeds if the leader is correct because the correct leader can pick up a correct view such that no other validator is locked on a conflicting chain.
Our solution
From the view of locking paradigm, in a bouncing attack, the attacker is misleading honest validators as if some honest validators are locked on it. Our solution simply uses a synchrony assumption that the delay of votes are up to k slots and hence votes delayed more than k can be considered adversarial when the network is normal.
Even when honest votes are actually delayed by a temporal network failure and some validators are locked on a checkpoint which you find justified more than k slots later, the protocol is stuck-free because validators can catch up at the start of the next epoch.
Notably, this approach is still leaderless and simple.
Future works
- Liveness proof of fixed FFG (Make sure that this fix does not introduce a new problem)
- Incentive analysis