This attack was subsequently published in: "Three Attacks on Proof-of-Stake Ethereum"
TL;DR: A previous post describes a balancing attack on Gasper, a model of Ethereum 2’s beacon chain. In that attack, the adversary uses adversarial network delay to break liveness. It was pointed out that “this attack does depend on networking assumptions that are highly contrived in practice (the attacker having fine-grained control over latencies of individual validators)”. This post documents a variant of the attack for which stochastic network delay suffices (as caused, for example, by stochastic message propagation in a peer-to-peer gossip network), making attacks of this flavor more practical. Simulations and experiments corroborate the findings.
The Ethereum 2 team has been informed and mitigation efforts are underway. For more information, see also this recent preprint, in particular Appendix I.
Motivation
The LMD variant of the GHOST fork choice rule is used alongside the finality gadget Casper FFG in the Gasper protocol to power the beacon chain (see here, here) and provide the foundation of Ethereum 2’s consensus mechanism. Earlier works (see here, here, here, here, here) have described various flavors of balancing-type attacks against variants of the GHOST fork choice rule. In particular, the attack described here and here employs adversarial network delay to show that Gasper is not secure in traditional synchronous and partially synchronous networks. While adversarial network delay (up to some known delay bound) as an assumption is commonly accepted and widely employed in the academic consensus literature, there is disagreement whether and to which degree it is reasonable in the context of Internet-scale open-participation consensus: “Note that this attack does depend on networking assumptions that are highly contrived in practice (the attacker having fine-grained control over latencies of individual validators), but nevertheless a protocol that is secure against such attacks is better than one that is not.”
This post documents how the earlier attack can be modified and implemented to obtain a more practical attack where an adversary can stall Gasper when it controls 15% of stake but without requiring adversarial network delay. To this end, we show through experiments that aggregate properties of many individually random message propagation processes (such as “within T time the message is received by roughly x fraction of participants”) in real-world Internet-scale peer-to-peer gossip networks are sufficiently predictable, to allow the adversary coarse but enough control over how many validators see which adversarial messages and when, to successfully launch variants of previous attacks. None of the adversarial actions are slashable protocol violations.
The high-level idea of the attack is sketched in the next section, followed by attack details, and method and results of an Internet-scale measurement of information propagation in peer-to-peer gossip networks. The resulting dataset was used as a model for network propagation delays in validating the attack via simulation. We conclude with comments on the applicability of the attack to Ethereum 2.
High-Level Idea
We assume that the reader is well-familiar with the balancing attack described here and here as well as its intellectual ancestors (see here, here, here). Recall in particular that the balancing attack consists of two steps: First, adversarial block proposers initiate two competing chains – let us call them Left and Right. Then, a handful of adversarial votes per slot, released under particular circumstances (this is where the adversarial network delay assumption enters that we would like to get rid of), suffice to steer honest validators’ votes so as to keep the system in a tie between the two chains and consequently stall consensus.
Given that we want to do away with fine-grained adversarial control over network delays, we look for other ways for the adversary to maintain the tie: What would honest validators do if they saw two competing chains with equal number of votes? If each node broke the tie by flipping a coin, roughly n/2 of n honest validators would vote Left and the other roughly n/2 would vote Right. In fact, the number of honest votes for Left and for Right would differ roughly in the order of \sqrt{n} (cf. the variance of a binomially distributed random variable). So if the adversary controls in the order of \sqrt{n} votes per slot, it could vote such as to restore the tie and keep the system in limbo. The crux is thus to get and keep the network in a state where roughly half of honest committee members vote Left and half vote Right, with a gap that the adversary can rebalance continuously.
According to Algorithm 3.1 of Gasper and the Ethereum 2 fork choice specification ties between two children blocks in LMD GHOST are not broken by a coin flip at each node individually, however, but globally consistent in favor of the block with smaller hash. Assume, without loss of generality, that the tie-break favors Left over Right. If the adversary manages to deliver an adversarial vote for Right from slot i-1 (or an earlier slot) to roughly half of honest validators for slot i, before the validators submit their votes for slot i, while the other half of honest validators does not receive said vote before the voting deadline, then roughly half of honest validators (those who have received the sway vote ‘in time’) see Left as leading and will vote for it in slot i, while the other half of honest validators (those who see the sway vote ‘late’ and hence at the time of voting see a tie which they break in favor of Right) will vote for Right in slot i. This process is illustrated in Figure 1.
Note that the time T_k it takes for a message to propagate via the peer-to-peer gossip network from the adversary to validator k is a random variable, rather than under adversarial control. However, the number of nodes in the network is large and so is the number of committee members per slot. Furthermore, the adversary does not have to control how each individual validator will vote – it suffices to produce a roughly equal split, so that the adversary can restore the balance with its adversarial committee members’ votes. Intuition about large probabilistic systems suggests that aggregate properties such as ‘how long does it take to reach roughly half of participants’ are fairly deterministic. Furthermore, since the adversary can observe votes cast by honest validators, and the adversarial behavior is not a slashable protocol violation, the adversary can adjust its estimate over time to obtain the time T_{\mathrm{delay}} by which it needs to send the sway vote before the voting deadline of slot i, so that honest validators get split evenly as best as possible.
Further below we provide evidence from real-world propagation delay measurements in a replica of Ethereum 2’s gossip network to support this hypothesis.
Detailed Description
First we describe the attack for a given T_{\mathrm{delay}}, then we describe techniques to estimate T_{\mathrm{delay}}. In the following, let \beta be the adversarial fraction of stake. A simulation (using the gossip network propagation model obtained from a measurement experiment described in the following section) of the attack can be found here.
First, the adversary waits for an opportune epoch to launch the attack. An epoch is opportune if the block proposers in slot 0 and 1 are adversarial. Due to the random committee selection, this happens with probability \beta^2 for any given epoch, so that the adversary needs to wait on average 1/\beta^2 epochs until it can launch the attack. (Note that this can be strengthened, as under some conditions the adversary can also launch the attack for two consecutive slots with adversarial proposer other than slots 0 and 1, but we stick with the above for ease of exposition.) In the following, assume epoch 0 is opportune.
The adversarial proposer of slot 0 proposes a new chain (‘Left’), and the adversarial proposer of slot 1 proposes a conflicting chain (‘Right’). Note that this is not a slashable violation of the protocol. Both withhold their proposals so that none of slot 0 or 1 honest validators vote for either of these blocks. The adversary releases the blocks to the network (and in particular to the validators of slot 2) after slot 1. We assume without loss of generality that the tie between Left and Right (recall that no vote has been cast for either so far) is broken in favor of Left.
Time T_{\mathrm{delay}} before honest validators in slot 2 cast their votes, the adversary releases a vote for Right from an adversarial committee member of slot 1 (so called sway vote, see Figure 1). If T_{\mathrm{delay}} is tuned well to the network propagation behavior at large, then roughly half of honest committee members of slot 2 see the sway vote before they cast their vote, and thus view Right as leading (due to the sway vote) and will cast a vote for Right, and half of honest committee members of slot 2 see the sway vote only after they cast their vote, and thus view Left as leading (due to the tie-break) and will cast a vote for Left. Once the adversary has observed the outcome of the vote, which now should be a split up to an order \sqrt{n} gap, the adversary uses its slot 2 committee members (in the order of \sqrt{n} many – which stipulates the adversarial fraction \beta required to launch this attack) as well as slot 0 and 1 committee members to rebalance the vote to a tie. (Note that slot 0 committee members can only vote for Left, as Right was only proposed in slot 1. Slot 1 committee members can vote for both Left or Right.) As the tie is restored, the adversary can use the same strategy in the following slot, and so forth.
How does the adversary obtain T_{\mathrm{delay}}? Note that the adversary can observe the outcome of a vote. This gives the adversary information about how many honest committee members saw Left and Right leading, respectively. If (after averaging over multiple attempts) the adversary observes a bias towards Left, then fewer than a half of committee members see the sway vote in time, hence the adversary should increase T_{\mathrm{delay}} (i.e., transmit earlier) for subsequent attempts. Vice versa, if there is a bias towards Right, then the adversary should decrease T_{\mathrm{delay}}. We show below that the optimal T_{\mathrm{delay}} can be reliably localized even using grid search.
Experimental Evaluation
To understand whether the network propagation delay distribution is sufficiently well-behaved for an adversary to reproducibly broadcast messages so that they arrive at roughly half of participants by a fixed deadline, we replicated the gossip network of Ethereum 2 and measured the network propagation delay of test ‘ping’ packets from a designated sender to all other participants. The implementation in the Rust programming language used libp2p's Gossipsub protocol and implementation, as is used in Ethereum 2.
The gossip network comprised 750 nodes, each on an AWS EC2 m6g.medium instance (with 50 instances each in all 15 AWS regions that supported m6g.medium as of 21-April-2021: eu-north-1, eu-central-1, eu-west-1, eu-west-2, ap-northeast-1, ap-northeast-2, ap-southeast-1, ap-southeast-2, ap-south-1, sa-east-1, ca-central-1, us-east-1, us-east-2, us-west-1, us-west-2). Each node initiated a connection with ten randomly chosen peers. The five nodes with lowest instance ID were designated as senders and continuously broadcasted beacon messages with inter-transmission times uniformly distributed between zero and five seconds, logging the time when each message was broadcast. All nodes logged the time when a beacon message was first received. The measurements were taken over a period of 20 minutes.
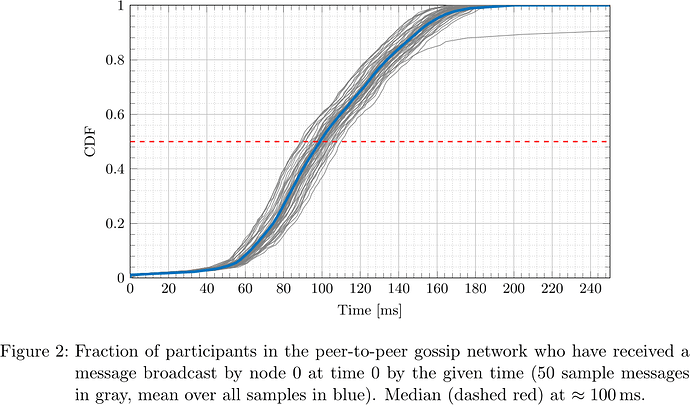
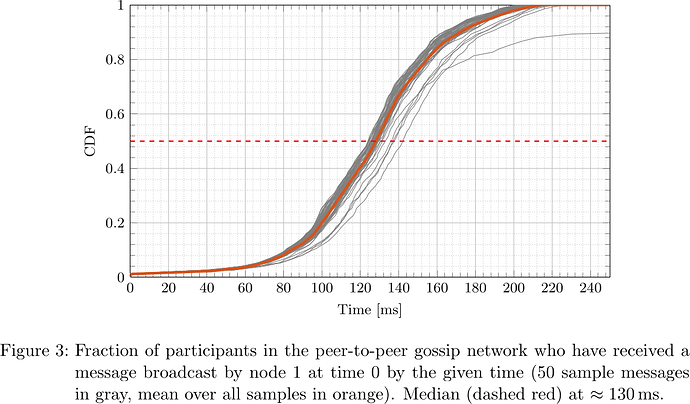
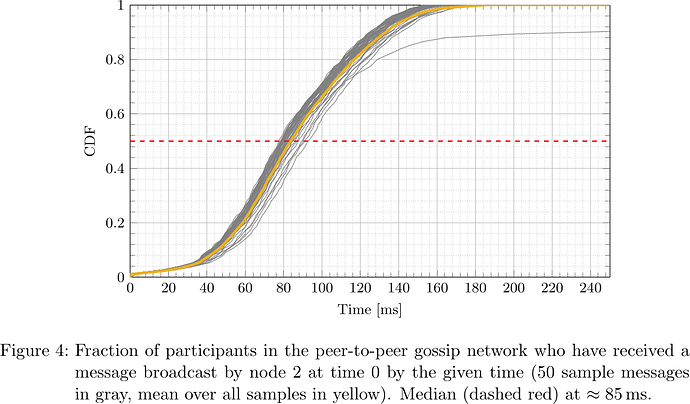
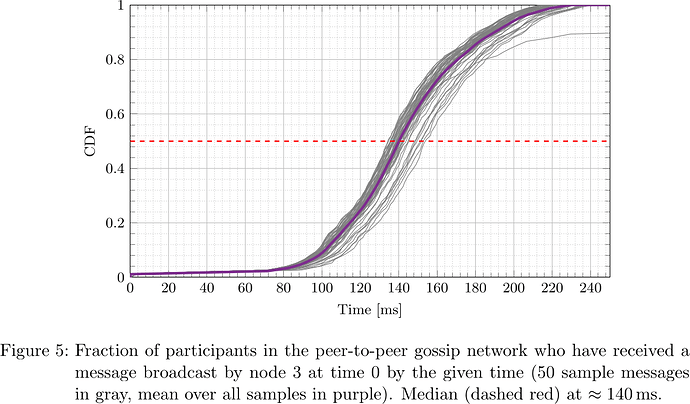
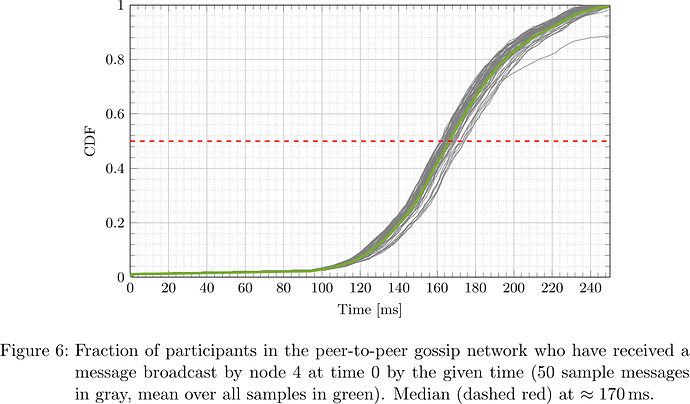
From the collected logs, the network propagation delay was determined for each message and each receiving participant. The respective cumulative distribution functions (CDFs), i.e., what fraction of participants had received the message by a certain time after sending, for the five designated senders are plotted in Figures 2–6.
It is apparent that depending on the location of the node (nodes 0, 1, 2, 3, 4 happened to be located in us-east-2, ap-northeast-1, us-east-1, ap-northeast-1, ap-northeast-2, respectively) both geographically as well as within the peer-to-peer network topology, the propagation delay distribution varies, but at the same time considering all messages originating at a fixed sender, the propagation delay distribution is fairly predictable. In particular, considering the median, that is the time at which half of participants have received a message and half have not, one sees that its distribution is fairly concentrated around the ‘average CDF’, suggesting that the adversary can indeed determine T_{\mathrm{delay}} such that with little dispersion honest validators get split in two halves.
We then simulated the attack for \beta=0.15, using the network propagation delay samples as a model for random network delay. (The source code can be found here.) In particular, after assigning the simulated adversary to one of the five designated senders for all of the attack, whenever the adversary broadcasts a sway vote, the propagation delay samples of a random message of the designated sender are selected, and for each honest committee members of the given slot the network delay is determined as a sample (without replacement) from the measured propagation delays to the 750 participants in the experiment for that particular message.
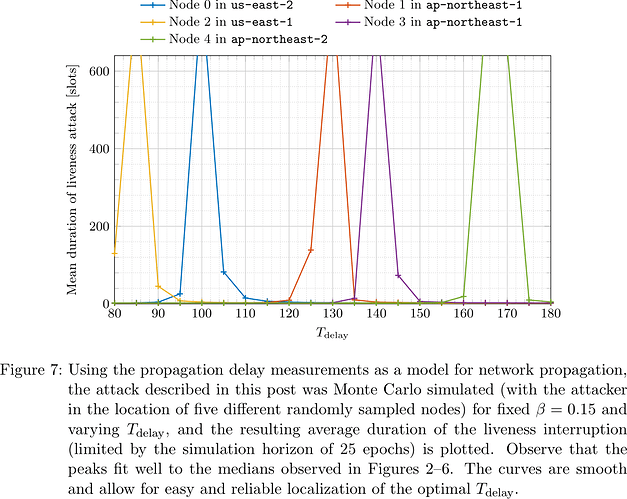
To determine the optimal T_{\mathrm{delay}}, we performed a grid search (with 5\,\mathrm{ms} step size) and for each T_{\mathrm{delay}} simulated the run of ten attack attempts in opportune epochs and recorded for how long the adversary was able to stall liveness (terminated at a horizon of 25 epochs, i.e., 800 slots). The result is plotted in Figure 7.
It is apparent that for the adversary in the position of each of the five designated senders of the measurement experiment, different T_{\mathrm{delay}} are optimal. The optimal T_{\mathrm{delay}} correspond well with the median of the ‘average CDF’ in Figures 2–6. As the curves are smooth and have a single distinct peak of width \approx5\,\mathrm{ms}, the adversary can locate the optimal T_{\mathrm{delay}} easily and reliably. In particular, even with T_{\mathrm{delay}} approximating the optimal value only up to 10\,\mathrm{ms}, the adversary can stall liveness for multiple epochs. Recall that none of the adversarial actions are slashable violations of the protocol, so that the adversary can launch this attack over and over again.
Application to Ethereum 2
A slight difference between Gasper and the Ethereum 2 beacon chain specification limits an immediate application of this attack to the Ethereum 2 beacon chain. While in Gasper validators vote at a fixed point in time (after half of a slot, see Definition 4.3 in Gasper), Ethereum 2 beacon chain validators vote “when either (a) the validator has received a valid block from the expected block proposer for the assigned slot or (b) one-third of the slot has transpired […] – whichever comes first” (see Section ‘Attesting’ here). As most proposers are honest, even during an attack, the adversary has no control and little information about when honest proposals will arrive at honest validators, and consequently when honest validators will cast their votes. (There is not a single dotted line as in Figure 1 anymore.) It is thus not as straightforward as in the case of Gasper to determine when the adversary needs to broadcast sway votes so as to achieve the desired roughly equal number of votes for Left and Right, respectively.
However, simulations based on the gossip propagation delay measurements suggest the following variant of the attack: Suppose the adversary controls a number of nodes at different ‘locations’ in the topology of the gossip network (these nodes might still be physically collocated). This is possible without greater difficulty because the gossip network has no defenses against such Sybil attacks. Then, some honest node will likely receive a new proposal pretty early on in the propagation process. How many adversarial nodes have already received the new proposal at what times gives the adversary information about how far the propagation process has progressed (think, in analogy to earthquakes, of the many adversarial nodes as an ‘early warning system’ for new proposals). The adversary can then release the sway vote in a coordinated fashion from all the different locations in the peer-to-peer topology where the adversary controls nodes, in such a way that ideally again roughly half of honest committee members receive the sway vote before they receive the proposal (and hence will vote according to the sway vote) and half receive the sway vote only after they receive the proposal (and hence will vote according to the tie break). Adversarial votes are used to rebalance and maintain a tie.
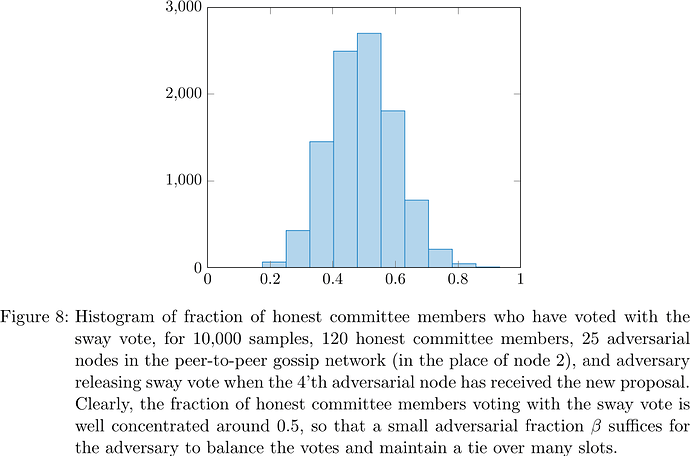
Simulations corroborate (see Figure 8) that indeed even with only 25 adversarial nodes, if the adversary releases the sway vote immediately after the 4'th adversarial node has received the new proposal for the current slot, then the adversary can control the fraction of honest committee members voting Left and Right, respectively, pretty well around one half, and rebalance to a tie with a small fraction of adversarial stake.